Il P-Value della somiglianza

Dati Voas

Dati Voas

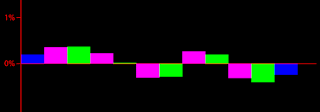
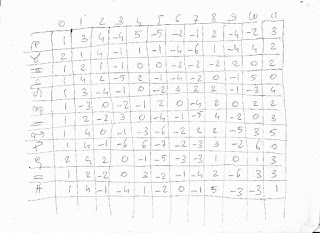
Ho aggiustato la tabella in modo che ci sia piena corrispondenza con il grafico delle deviazioni riportato in alto. In pratica ho solo invertito le colonne all'interno dei cinque aspetti doppi. Inoltre questa volta ho inserito nella tabella anche i totali delle singole colonne.

I totali delle colonne che appartengono allo stesso aspetto riportano dei risultati che sono molto simili tra loro. La cosa si vede anche ad occhio, le deviazioni per lo stesso aspetto sono molto simili tra loro. Le deviazioni colorate in rosa in cui il segno del marito precede quello della moglie sono molto simili a quelle colorate in verde in cui il segno del marito segue quello delle mogli.

Se prendiamo i 10 valori dei 5 aspetti doppi, e li disegniamo su una linea orizzontale che va da -33 a + 30, diventa chiaro che il modo in cui sono accoppiati questi valori, è uno dei modi migliori in cui potrebbero essere accoppiati.

Supponiamo di non essere in grado di stabilire la significatività statistica delle singole colonne, che poi in parte è vero, perché riesco a calcolare il P-Value di questo tipo di deviazioni solo in modo approssimativo.

Notiamo che ci sono delle deviazioni che vanno da -33 a + 30, ma non sappiamo dire se queste deviazioni siano significative oppure no. Possiamo però calcolare il P-Value della somiglianza tra le colonne dello stesso aspetto.

Questa somiglianza tra le colonne dello stesso aspetto, è importante perché è anch'essa una dimostrazione che i valori riportati nella tavola n.8 di Voas non sono affatto casuali.

Questo P-Value, ad una coda,  è uguale a P = 0,005 e questo significa che avevamo solo 1 probabilità su 200 che si verificasse una somiglianza tra le colonne dello stesso aspetto uguale o maggiore di quella riscontrata. Per cui è piuttosto probabile che questa somiglianza non sia l'effetto di un caso, e che i totali di ciascuna colonna assomiglino a quelli della colonna dello stesso aspetto, perché è proprio l'aspetto che produce quel tipo di deviazione.

Era così difficile?

12 Aspetti

7 Aspetti

Qui abbiamo preso i valori della tavola n.8 di Voas, e abbiamo creato due nuove tabelle dove le coppie sono raggruppate secondo l'aspetto formato dai segni di nascita dei coniugi.

Le deviazioni riscontrate per gli aspetti sono estremamente significative.

Quei numeri che si leggono nell'ultima riga della seconda tavola non potrebbero essere così alti se si trattasse di deviazioni casuali. In particolare sono molto significativi i deficit che si riscontrano per le coppie in quadratura e in quinconce.

Nonostante Voas abbia eliminato l'eccesso delle coppie in congiunzione, non è riuscito ad eliminare il deficit delle coppie in quadratura e in quinconce.

Le coppie in quadratura e in quinconce sono molto meno di quelle che dovrebbero essere, per cui possiamo concludere che c'è qualcosa che fa si che le persone i cui segni formano questi aspetti tendono a sposarsi meno frequentemente del previsto.

L'intelligenza delle mani

Io ancora disegno gli oroscopi a mano. Se una carta del cielo mi interessa particolarmente faccio i calcoli con il computer, ma poi disegno il grafico a mano. Mi aiuta a concentrarmi, disegnare Marte al 25esimo grado dello Scorpione, è diverso da vedere Marte al 25esimo grado dello Scorpione. E' solo nel momento in cui traccio il simbolo di Marte in un oroscopo, che mi rendo conto che Marte stava proprio lì dove lo disegno, e non da un'altra parte. Ed è solo in questo momento che incomincio a chiedermi  PERCHE' Marte è proprio in quella posizione, e che cosa significa per il consultante.

I simboli dei segni e dei pianeti che disegno a mano, sono diversi da quelli di un grafico computerizzato.

Se non disegno l'oroscopo alla mia maniera, non mi ci trovo, perché non sto utilizzando i miei simboli.

Con il passare degli anni ho modificato il modo di scrivere i segni zodiacali, così come avviene per la scrittura. A scuola si apprende un modello, ma poi ognuno scrive in un modo personale, allontanandosi da questo modello.

Ho riflettuto sul mio modo di scrivere i segni zodiacali, e questo mi ha permesso di capire alcune cose che non avevo ben compreso prima. Il mio modo di disegnare i simboli zodiacali richiama molto gli organi del corpo umano a cui il segno è associato. Ad esempio rappresento il segno del Cancro come un seno, e il segno dello Scorpione come l'organo sessuale maschile a riposo. Il segno del Capricorno lo disegno come un ginocchio, il segno della Bilancia come un paio di reni, il segno dell'Ariete come un cervello, e quello della Vergine come un pugno chiuso.

Comunque credo che i mie segni disegnati a mano siano comprensibilissimi per gli altri astrologi, perché non mi sono allontanato più di tanto dal modello che viene proposto, però io mi accorgo di questa personalizzazione che ho attuato inconsapevolmente, e che mi porta a disegnare delle parti del corpo umano al posto dei simboli classici.

Come se la mia mano avesse capito prima della mia mente, il legame che c'è tra i segni e la fisiologia umana.  

E' per questo che vi chiedevo di disegnare la tabella aspetti. Vi suggerivo di sfruttare l'intelligenza delle vostre stesse mani.

Un conto è se io vi racconto una cosa, ed un altro se la verificate da soli con le vostre mani.

Disegnare a mano questa tabella vi aiuterebbe a capire qualcosa che sarebbe più difficile da capire se ve lo spiegassi.