Simulazioni statistiche

Clicca sull'immagine

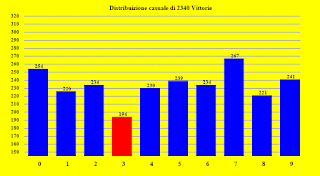
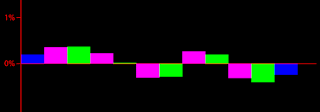
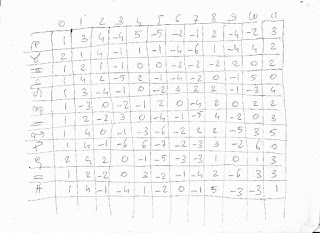
Ho creato una pagina che distribuisce in modo casuale le 2340 vittorie nelle 10 fasi.

Se una di queste fasi è significativa al livello dello 1%, allora viene colorata in rosso, sia se si tratta di un eccesso, sia se si tratta di un deficit.

Cliccando ripetutamente sul pulsante refresh, avete modo di rendervi conto da soli quante volte si verifica che almeno una delle colonne mostra una deviazione significativa. Non si tratta affatto di qualcosa che avviene raramente, perché capita mediamente un po' meno di una volta su 10.

La cosa divertente è che Ruscelli non ha sbagliato solo questa statistica, ma praticamente tutte le sue statistiche nel corso degli ultimi quarant'anni. Perché commette sempre questo stesso errore che lo porta a sovrastimare la significatività statistica, e quindi a trovare delle correlazioni astrologiche quando queste in realtà non ci sono.

Ecco spiegata la differenza che trova nelle sue statistiche basate sul sesso.

Se per gli uomini risulta significativa una fase, e per le donne un'altra, è perché gli eccessi che riscontra nell'una e nell'altra statistica sono casuali.

Ma voi avete mai sentito che Giove in X casa è favorevole per la carriera degli uomini, mentre per le donne la casa favorevole al successo è la quinta?

Io non ho mai notato delle differenze basate sul sesso, con l'astrologia si legge l'anima delle persone, e le anime non hanno sesso.

Certo, ci sono alcune differenze basate sul sesso. Ad esempio una donna che ha molti partner sessuali, di solito non viene giudicata positivamente, al contrario di quello che succede per un uomo. Ma queste differenze che si riscontrano nei due sessi, sono di tipo adattativo, non sono delle differenze sostanziali.

E' giusto interpretare una carta del cielo tenendo conto del sesso di una persona, ma l'influsso astrologico in se, è indipendente dal sesso.

Un errore imperdonabile

Nella tabella qui sopra ci sono i risultati ottenuti da Gabriele Ruscelli in una statistica pubblicata sul numero 183 di Linguaggio Astrale (estate 2016). In pratica con questa sua ricerca Ruscelli intendeva verificare se i politici vincono più frequentemente le elezioni durante una delle 10 fasi del loro personale ciclo sinodico di Giove.

L'ipotesi di partenza
Esiste almeno una fase del ciclo sinodico di Giove durante la quale si verifica un frequenza significativamente elevata di elezioni politiche, per i politici di entrambi i sessi, calcolando il periodo sinodico a partire dalla data di nascita del politico.

Già su questa ipotesi ci sarebbe qualcosa da obiettare. Se Ruscelli crede che esista una relazione tra il ciclo di Giove e le vittorie elettorali, dovrebbe chiedersi se i risultati da lui ottenuti si discostano nel loro insieme da quelli che sono i risultati prevedibili, e se lo fanno in modo statisticamente significativo.

Non si capisce perché parli di frequenza significativamente elevata, visto che una frequenza significativamente bassa, avrebbe comunque la capacità di farci sospettare una relazione tra il ciclo di Giove e le vincite elettorali.

Certo, è naturale, di solito l'attenzione si rivolge più verso gli eccessi che verso i deficit. Però bisognerebbe tenere a mente che se esistesse realmente un influsso astrale legato al ciclo di Giove, questo influsso creerebbe tanto degli eccessi che dei deficit. Perché ovviamente i casi in eccesso che si producono per una fase, sono dei casi in deficit di un'altra fase.

Ma come si fa a sapere se i risultati trovati si discostano in modo significativo dai risultati attesi?

Basta inserire i risultati in questo sito di statistiche.

Ma prima di inserire in questo sito i risultati trovati vi suggerirei di inserire questi risultati.

Il sito ci dice che i risultati trovati sono estremamente statisticamente significativi, con una probabilità che questi risultati siano frutto di un caso molto bassa pari a 0,0007, per cui ci sarebbero solo 7 casi su 10.000 che questi risultati siano frutto di un caso. Eppure, nessuna di queste fasi mostra una deviazione significativa se presa singolarmente. Per cui Ruscelli con questi risultati avrebbe detto che la sua ipotesi non si era realizzata, sebbene l'insieme della tabella mostra un probabilissimo effetto astrologico.

In assenza di ipotesi precise, la cosa migliore da fare è quello di valutare la significatività statistica generale della tabella ottenuta.

Adesso provate ad inserire i risultati realmente ottenuti nel sito e leggete il responso.

Il responso è che le deviazioni trovate per questa tabella non sono significative, perché ci sono circa 12 probabilità su 100 di ottenere delle deviazioni come queste, o maggiori di queste, per un semplice caso.

Naturalmente io non posso imporre la mia ipotesi a Ruscelli, anche se trovo la sua ipotesi poco razionale.

L'ipotesi di Ruscelli in realtà si verifica. Nella fase n.1 della tabella in alto ci sono 278 vittorie mentre il numero atteso era di 234 vittorie.

Ma come si fa a sapere se questo risultato è significativo, e quanto è significativo?

Lo si può sapere utilizzando sempre lo stesso sito. Inserendo i dati della fase n.1 , e quindi 278 come numero trovato e 234 come numero atteso, e creando una nuova categoria che comprende tutti gli altri risultati.

Per cui il numero trovato per questa nuova categoria è dato dal numero totale delle vittorie meno quelle del settore n.1, e il numero atteso è 234 * 9 = 2106.

P value and statistical significance:
Chi squared equals 9.193 with 1 degrees of freedom.
The two-tailed P value equals 0.0024
By conventional criteria, this difference is considered to be very statistically significant.

Per cui il sito ci conferma che quella riscontrata per la fase n.1 è una deviazione significativa e che ci sarebbero solo 2 probabilità su 1000 che questo si sia verificato per caso. Ruscelli, chissà perché, calcola una probabilità leggermente diversa, perché dice che ci sarebbero 4 probabilità su 1000 che questa deviazione si sia verificata per un puro caso. Questa discrepanza non è molto importante, perché comunque l'ordine di grandezza è lo stesso, e se la probabilità è di 2 casi su 1000 o di 4 casi su 1000, non cambia molto.

Ma a cosa si riferisce questa probabilità?

Questa è la probabilità che nella fase n.1 si verificasse una simile deviazione.

Non è la probabilità corrispondente all'ipotesi di Ruscelli.

L'ipotesi di Ruscelli era che almeno per una fase, delle 10 fasi, avrebbe trovato un risultato significativo,
come in effetti è poi avvenuto. Ma la probabilità di questo evento non è quella relativa alla fase n.1.

Questa probabilità andrebbe presa in considerazione se Ruscelli avesse ipotizzato che avrebbe trovato una deviazione importante proprio per questa fase.

Ma l'ipotesi di Ruscelli era generica, non riguardava in modo specifico questa fase n.1, ma coinvolgeva tutte e 10 le fasi che potenzialmente potevano mostrare una deviazione significativa come questa.

In altre parole, se Ruscelli invece di trovare 278 vittorie per la fase n.1, le avesse trovate per la fase n.3 o per la fase n.5, lui sarebbe comunque andato alla cassa per reclamare la sua vincita, perché lui ha scommesso su tutte e 10 le fasi, e non su una fase in particolare.

E quindi qual è la vera probabilità associata all'ipotesi di Ruscelli?

E' molto semplice, è 10 volte la probabilità della fase n.1.

Per cui, è vero che l'ipotesi di Ruscelli si sia verificata, ma la probabilità che questo sia avvenuto per un semplice caso è di 2 casi su 100 e non di 2 casi su 1000.

Per cui la significatività trovata è piuttosto bassa raggiungendo soltanto il livello del 5%.

Immaginate di andare a giocare alla roulette e di puntare 10 euro su un certo numero.
La probabilità di vincita è di 1/37 e se il vostro numero esce il banco vi paga 360 euro.

Se invece puntate 1 euro su 10 numeri diversi, la vostra probabilità di vittoria è di 10/37, e
se uno di questi numeri esce il banco vi da 36 euro, perché su quel numero avete puntato solo un euro.

Ruscelli punta su 10 numeri, e uno di questi effettivamente esce, però non può pretendere una vincita di 360 euro perché gliene spettano solo 36, perché lui avevo distribuito la sua puntata su 10 numeri diversi, e non aveva puntato tutto il suo capitale sull''unico numero che poi è uscito.

Si tratta di logica elementare, e non capisco come ci sia qualcuno che non comprende queste cose.

Il P-Value della somiglianza

Dati Voas

Dati Voas

Ho aggiustato la tabella in modo che ci sia piena corrispondenza con il grafico delle deviazioni riportato in alto. In pratica ho solo invertito le colonne all'interno dei cinque aspetti doppi. Inoltre questa volta ho inserito nella tabella anche i totali delle singole colonne.

I totali delle colonne che appartengono allo stesso aspetto riportano dei risultati che sono molto simili tra loro. La cosa si vede anche ad occhio, le deviazioni per lo stesso aspetto sono molto simili tra loro. Le deviazioni colorate in rosa in cui il segno del marito precede quello della moglie sono molto simili a quelle colorate in verde in cui il segno del marito segue quello delle mogli.

Se prendiamo i 10 valori dei 5 aspetti doppi, e li disegniamo su una linea orizzontale che va da -33 a + 30, diventa chiaro che il modo in cui sono accoppiati questi valori, è uno dei modi migliori in cui potrebbero essere accoppiati.

Supponiamo di non essere in grado di stabilire la significatività statistica delle singole colonne, che poi in parte è vero, perché riesco a calcolare il P-Value di questo tipo di deviazioni solo in modo approssimativo.

Notiamo che ci sono delle deviazioni che vanno da -33 a + 30, ma non sappiamo dire se queste deviazioni siano significative oppure no. Possiamo però calcolare il P-Value della somiglianza tra le colonne dello stesso aspetto.

Questa somiglianza tra le colonne dello stesso aspetto, è importante perché è anch'essa una dimostrazione che i valori riportati nella tavola n.8 di Voas non sono affatto casuali.

Questo P-Value, ad una coda,  è uguale a P = 0,005 e questo significa che avevamo solo 1 probabilità su 200 che si verificasse una somiglianza tra le colonne dello stesso aspetto uguale o maggiore di quella riscontrata. Per cui è piuttosto probabile che questa somiglianza non sia l'effetto di un caso, e che i totali di ciascuna colonna assomiglino a quelli della colonna dello stesso aspetto, perché è proprio l'aspetto che produce quel tipo di deviazione.

Era così difficile?

12 Aspetti

7 Aspetti

Qui abbiamo preso i valori della tavola n.8 di Voas, e abbiamo creato due nuove tabelle dove le coppie sono raggruppate secondo l'aspetto formato dai segni di nascita dei coniugi.

Le deviazioni riscontrate per gli aspetti sono estremamente significative.

Quei numeri che si leggono nell'ultima riga della seconda tavola non potrebbero essere così alti se si trattasse di deviazioni casuali. In particolare sono molto significativi i deficit che si riscontrano per le coppie in quadratura e in quinconce.

Nonostante Voas abbia eliminato l'eccesso delle coppie in congiunzione, non è riuscito ad eliminare il deficit delle coppie in quadratura e in quinconce.

Le coppie in quadratura e in quinconce sono molto meno di quelle che dovrebbero essere, per cui possiamo concludere che c'è qualcosa che fa si che le persone i cui segni formano questi aspetti tendono a sposarsi meno frequentemente del previsto.

L'intelligenza delle mani

Io ancora disegno gli oroscopi a mano. Se una carta del cielo mi interessa particolarmente faccio i calcoli con il computer, ma poi disegno il grafico a mano. Mi aiuta a concentrarmi, disegnare Marte al 25esimo grado dello Scorpione, è diverso da vedere Marte al 25esimo grado dello Scorpione. E' solo nel momento in cui traccio il simbolo di Marte in un oroscopo, che mi rendo conto che Marte stava proprio lì dove lo disegno, e non da un'altra parte. Ed è solo in questo momento che incomincio a chiedermi  PERCHE' Marte è proprio in quella posizione, e che cosa significa per il consultante.

I simboli dei segni e dei pianeti che disegno a mano, sono diversi da quelli di un grafico computerizzato.

Se non disegno l'oroscopo alla mia maniera, non mi ci trovo, perché non sto utilizzando i miei simboli.

Con il passare degli anni ho modificato il modo di scrivere i segni zodiacali, così come avviene per la scrittura. A scuola si apprende un modello, ma poi ognuno scrive in un modo personale, allontanandosi da questo modello.

Ho riflettuto sul mio modo di scrivere i segni zodiacali, e questo mi ha permesso di capire alcune cose che non avevo ben compreso prima. Il mio modo di disegnare i simboli zodiacali richiama molto gli organi del corpo umano a cui il segno è associato. Ad esempio rappresento il segno del Cancro come un seno, e il segno dello Scorpione come l'organo sessuale maschile a riposo. Il segno del Capricorno lo disegno come un ginocchio, il segno della Bilancia come un paio di reni, il segno dell'Ariete come un cervello, e quello della Vergine come un pugno chiuso.

Comunque credo che i mie segni disegnati a mano siano comprensibilissimi per gli altri astrologi, perché non mi sono allontanato più di tanto dal modello che viene proposto, però io mi accorgo di questa personalizzazione che ho attuato inconsapevolmente, e che mi porta a disegnare delle parti del corpo umano al posto dei simboli classici.

Come se la mia mano avesse capito prima della mia mente, il legame che c'è tra i segni e la fisiologia umana.  

E' per questo che vi chiedevo di disegnare la tabella aspetti. Vi suggerivo di sfruttare l'intelligenza delle vostre stesse mani.

Un conto è se io vi racconto una cosa, ed un altro se la verificate da soli con le vostre mani.

Disegnare a mano questa tabella vi aiuterebbe a capire qualcosa che sarebbe più difficile da capire se ve lo spiegassi.

Esercizio

Tavola n.8

Ordinare i risultati della tavola n.8 di Voas in base agli aspetti, e calcolare i totali di ciascun aspetto.


Un metodo potrebbe essere quello di lasciare invariata la colonna delle wife e cancellare la riga degli husband per sostituirli con 0, 1, 2, 3 ..11.

La prima riga, quella delle donne Ariete si può lasciare così, mentre la seconda riga relativa al Toro deve slittare di un posto. Cioè il risultato che si trova all'incrocio Toro-Toro deve diventare il primo della riga, mentre il risultato che ora è il primo della riga viene scalzato all'ultimo posto.
E poi si procede con lo stesso metodo per le righe successive.

Una volta ottenuta la tavola con 12 aspetti si possono raggruppare insieme gli aspetti simili.

0    Congiunzione

1 e 11 Semisestile

2 e 10 Sestile

3 e 9 Quadratura

4 e 8 Trigono

5 e 7 Quinconce

6   Opposizione

Ottenendo cosi una tavola di sette aspetti dalla congiunzione (0) all'opposizione(6).

Un ordine evidente

Tavola dati Voas

A pagina 12 della voasastrology Voas scrive:

The nature of commissioned table C0792 makes it possible to carry out at least two further types of test. First, one can compare sets of birthdays defined not only by sun sign or month, but on any basis at all. Unless the discrepancies between the actual and expected counts are larger and more systematic when using sun sign rather than other groupings, there is no evidence to support their alleged influence.

Secondly, C0792 provides a full breakdown of spousal dates of birth by age of husband. There are four broad age groups of roughly similar size: under 40, 40-49, 50-64, and 65 and over. Only if the pattern of deviations (as shown in Table 8) is the same in all four groups would it suggest that the discrepancies are non-random.

Qui Voas dice che la tavola da lui commissionata allo ONS, e che contiene il numero dei matrimoni per ciascuna delle 366 x 366 combinazioni del giorno di nascita dei coniugi, ci permette di raggruppare le coppie in modi diversi, e che solo se le deviazioni riscontrate con i segni sono più grandi e più sistematiche di quelle ottenute con altri raggruppamenti, questo sarebbe una prova a favore dell'influsso dei segni.

Poi Voas dice che ha anche quattro sottogruppi della statistica, basati sulle fasce di età dei mariti.
Il fatto di avere i dati raggruppati per età, permetterebbe di confrontare le deviazioni che si riscontrano nei 4 gruppi, e di verificare se queste deviazioni sono simili. Se questo si verificasse, la cosa farebbe pensare che le deviazioni non siano casuali.

Ma Voas non effettua questi test.

Io il primo test l'ho eseguito, ossia ho provato a vedere se invece di considerare i segni zodiacali normali, se ne utilizzano altri fittizi. Ma di questo ne parlerò in seguito.

Per quanto riguarda il secondo test, lui ha i dati divisi anche per fascia di età (dei mariti) ma io non ho questi dati, per cui non potrei fare questo test. Ma ciò che dice è giusto, se le quattro cartelle mostrassero delle deviazioni simili, questo rafforzerebbe molto l'idea di un influsso astrologico.

Quello che non si capisce è perché non applica questo stesso principio ai risultati della statistica complessiva.

Il punto di forza della mia statistica, è dato proprio dal fatto che i segni mostrano tutti un comportamento simile. Gli Ariete, i Toro, i Gemelli ecc. hanno tutti un comportamento simile: Vanno d'accordo con se stessi, e non vanno d'accordo con i segni in quadratura, quinconce, e opposizione.

Prima di pensare alle sue cartelle divise per fasce di età, avrebbe dovuto pensare alla divisione in 12 sottogruppi della cartella principale.

C'è già una suddivisione naturale in 12 sottogruppi nella cartella principale, perché i segni sono 12.
Per cui possiamo andare a vedere che cosa fa l'Ariete con i suoi segni in quadratura, e poi confrontarlo con come si comporta il Toro con i suoi segni in quadratura, e confrontarlo con come si comporta il Gemelli, con i suoi segni in quadratura.

I SEGNI SI COMPORTANO TUTTI NELLA STESSA MANIERA a parte delle piccole variazioni casuali.

Dai dati della statistica possiamo estrapolare una legge a carattere generale, ciascun segno va d'accordo con se stesso, e non va d'accordo con i segni in quadratura, quinconce, e opposizione.

Questa regola ha pochissime eccezioni se si guarda ad uno specifico segno.

Tutto ciò è una ulteriore conferma delle deviazioni trovate, perché la regola generale è confermata dai 12 "sottogruppi", ed è lo stesso Voas a dirci, che quando questo si verifica sia ha la conferma che i risultati non sono random.

Ma veramente ci vorrebbe un esperto?

I dati mostrati nell'immagine qui sopra non sono sufficienti?

Quell'immagine riporta i risultati elaborati da Voas nella sua tavola n.7 e che gli fa concludere che non c'è un influsso dei segni sull'amore.

Io mi sono limitato a "raddrizzare" le diagonali della sua tavola n.7, trasformandole in colonne.

A ciascuna di queste colonne corrisponde quindi un aspetto. L'aspetto 0 è la congiunzione e a seguire abbiamo nell'ordine il semisestile, il sestile, la quadratura, il trigono, il quinconce e l'opposizione.

Il grafico mostra che gli aspetti tendono ad avere un colore predominante, come se ci fosse un influsso che rende favorevole o sfavorevole questo aspetto.

In una distribuzione casuale non dovrebbe essere così, le caselle celesti e le caselle rosse dovrebbero essere sparpagliate alla rinfusa in quella tavola. Al contrario c'è un ordine molto evidente.