Pacchetto da 10

Non mi date soddisfazione. Finora non c'è stato ancora un blogger che abbia scritto di aver compreso in che consiste l'errore di Ruscelli. Eppure non mi sembra una cosa tanto complicata.

Ho creato una nuova pagina, dove invece che una simulazione alla volta, ne vengono proposte 10 tutte assieme.

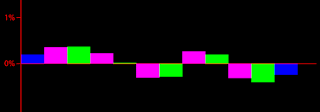
Di solito, caricando o ricaricando questa pagina dovreste vedere 1 fase colorata in rosso, anche se qualche volta può capitare che non ne vediate alcuna, così come può capitare che ne vediate più di una.

Le fasce sono colorate in rosso quando mostrano una significatività dello 1%.

Una significatività dello 1% significa che ci aspettiamo di trovare una deviazione del genere circa 1 volta su 100.

Ma allora come mai in questo pacchetto di 10 simulazioni, molto spesso riscontriamo che c'è una fase in rosso? Non dovremmo trovare una fase in rosso, ogni 100 simulazioni? Perché di solito ne bastano solo 10 perché spunti da qualche parte una fascia colorata in rosso?

La risposta è molto semplice. La significatività dello 1%, riguarda quella specifica fascia colorata in rosso.

Se ad esempio la fascia colorata in rosso è la n.1, questo significa che la fascia n.1 sarà colorata in rosso circa 1 volta su 100.

Ma la probabilità di trovare una fascia qualsiasi delle 10, colorata in rosso è 10 volte quella della fascia n.1.

Il pacchetto di 10 simulazioni che vi ho proposto in questa pagina, contiene 100 fasce, per cui è normale che su 100 fasce ce ne sia 1 che risulti significativa al livello dello 1%. Perché è proprio questo quello che ci aspettiamo.

Per cui su 10 simulazioni, ci aspettiamo che ci sia una fascia colorata in rosso.

Bisogna tener presente che siccome stiamo parlando di simulazioni, il risultato di queste simulazioni non potrà mai essere significativo, per cui si parla sempre di falsi positivi, che sembrano indicare come favorevole ora una fascia, ora un'altra.

Visto che ogni 10 simulazioni si presenta un falso positivo, se troviamo nella realtà una fascia significativa allo 1%, non abbiamo motivo di credere che non sia l'effetto di un caso. E comunque la probabilità che questo si verifichi è del 10% e non dello 1%.

Il Ciclo Sinodico di Giove

A quanto pare, nonostante le mie spiegazioni, questa storia della statistica non è ben chiara a tutti. Penso che non sia giusto scannarsi per questo, o prendere una posizione a favore di una tesi o dell'altra, sulla base delle proprie antipatie o simpatie. Non è necessario fare così, perché con un po' di impegno, tutti possono capire di cosa si sta parlando, anche senza essere degli esperti di matematica e statistica.

Ruscelli ha fatto una statistica in cui ipotizza che ci possa essere una relazione tra il ciclo sinodico di Giove e le vittorie elettorali dei politici uomini e dei politici donne analizzati separatamente.

Non è il caso di spiegare in dettaglio che cosa sia questo ciclo sinodico di Giove. Per sommi capi, siccome la Terra compie una rivoluzione intorno al Sole in un anno, e siccome Giove nello stesso tempo percorre circa un segno zodiacale, tra una congiunzione Sole-Giove e quella successiva passano circa 13 mesi. Perché la Terra impiega un anno per tornare nella stessa posizione in cui si trovava un anno prima, e circa un altro mese per raggiungere Giove che nel frattempo si è spostato ed è avanzato di un segno.

Ruscelli nella sua relazione scrive che la durata media di questo periodo è di 398,88 giorni. Non ho controllato questo dato, perché mi fido.

Ognuno di noi nasce in un certo momento del ciclo Sole-Giove, c'è chi nasce durante la congiunzione, c'è chi nasce durante l'opposizione, e in qualsiasi altra fase.

Il ciclo sinodico personale di Giove inizia per ciascuno di noi, quando nello zodiaco si riproduce la stessa distanza angolare tra il Sole e Giove che questi due corpi celesti formavano nel giorno in cui siamo nati.
Quando questo avviene entriamo nella nostra personale fase n.0 del ciclo gioviano.

Invece di andare a vedere con le effemeridi alla mano quando si riproduce esattamente lo stesso angolo tra il Sole e Giove che questi due corpi celesti formavano alla nascita, Ruscelli suggerisce un metodo semplificato basato sul periodo medio di 398,88 giorni che intercorre tra una congiunzione e quella successiva.

Lui calcola il numero dei giorni che sono trascorsi dalla nascita di un uomo politico e il giorno in cui ha vinto le elezioni, e divide questo numero per 398,88. Del quoziente così ottenuto, ignora la parte intera, e sofferma la sua attenzione sulla prima cifra dopo la virgola.  La cifra così ottenuta, è la cifra che indica la fase del ciclo gioviano in cui è avvenuta questa vittoria elettorale.

Io trovo questo metodo simpatico. Non so fino a che punto ci possa essere corrispondenza tra le fasi del ciclo gioviano calcolate in questo modo, e quelle che si potrebbero calcolare con un altro metodo, che tenga conto delle effettive posizioni del Sole e di Giove, sia alla nascita, che nel giorno della vittoria elettorale.

In generale l'astronomia non funziona con i valori medi. Il Sole per tornare nella stessa posizione impiega più o meno sempre lo stesso tempo, ma per Giove le cose sono un po' diverse, perché quando è in prossimità del suo perielio si muove più velocemente, mentre quando è vicino al suo afelio si muove più lentamente, e questo potrebbe complicare le cose.

La questione andrebbe approfondita, però al momento questo non ha grande importanza, e comunque il metodo di Ruscelli per definire le fasi gioviane, è fondamentalmente corretto.

La questione importante è un'altra. Le fasi gioviane definite col metodo appena spiegato, hanno un significato astrologico? Esiste realmente una correlazione tra queste fasi del ciclo personale sinodico di Giove e le vittorie elettorali dei politici?

La statistica di Ruscelli ha proprio lo scopo di appurare l'esistenza di questa correlazione.

Per cui dal prossimo post entrerò nel vivo della statistica.
     

Chiederò al CICAP

Ho intenzione di fotocopiare la statistica di Ruscelli e di sottoporla al vaglio del CICAP.

Gli dirò: Gli astrologi sostengono che esiste una relazione tra il ciclo sinodico di Giove e le vittorie elettorali dei politici, e sostengono di averlo dimostrato per mezzo di una statistica. Voi cosa ne pensate? Le cose stanno veramente così?

Gli dirò esattamente così: "Gli astrologi".

Non gli dirò Gabriele Ruscelli sostiene di aver dimostrato un influsso astrologico per mezzo di una statistica, ma gli dirò che a fare questa affermazione sono TUTTI GLI ASTROLOGI.

Perché?

Perché questa statistica è stata pubblicata su Linguaggio Astrale che è la rivista di astrologia più importante esistente oggi in Italia. Che io sappia, nessuno dei lettori di questa rivista ha trovato qualcosa da obiettare su questa statistica, e quindi, evidentemente, TUTTI GLI ASTROLOGI, ne condividono le conclusioni.

Non so se qualcuno del CICAP avrà voglia di commentare questa statistica, può darsi di si, come può darsi di no. Quello che so è che farò le fotocopie della statistica e che chiederò gentilmente a qualcuno del CICAP di esaminarla.

Gabriele Ruscelli ritiene che io sia un maleducato perché mi sono permesso di evidenziare l'errore evidente che essa contiene. Perché dovrebbe essere una questione di maleducazione?

Per criticare le statistiche di Ruscelli occorre l'approvazione della Sacra Rota?

Non ho rispettato l'etichetta?  Ho infranto qualche regola del galateo?

Perché dire che 2 + 2 non fa 5 ma fa 4 dovrebbe essere da maleducati?

Io mi sono limitato a dire che i calcoli statistici presenti in quella relazione sono errati, per il semplice motivo che quei calcoli sono oggettivamente errati.

Non ho attaccato Ruscelli personalmente, non ho parlato di lui, ma della sua statistica.

Lui invece attacca me personalmente, mi da del maleducato, cercando di offendere non solo me, ma anche i miei genitori che si suppone siano quelli che mi avrebbero dovuto impartire una educazione.

Ruscelli non prova nemmeno a contestare le mie critiche, non dice non è come dici tu perché così, così, così.

Lui dice tu non sei degno di una mia risposta, sei un miserabile, quando in realtà è il suo comportamento ad essere da miserabile.

Io me ne frego del tentativo di Ruscelli di lanciarmi della melma addosso. I suoi giudizi hanno lo stesso valore delle sue statistiche, ossia nessuno.

Le sue statistiche sono il riflesso della sua intelligenza, e il suo modo di reagire alle critiche, cercando di delegittimare i suoi interlocutori, è il riflesso della sua mediocrità e della sua vigliaccheria che è il tratto dominante della sua personalità.

Simulazioni statistiche

Clicca sull'immagine

Ho creato una pagina che distribuisce in modo casuale le 2340 vittorie nelle 10 fasi.

Se una di queste fasi è significativa al livello dello 1%, allora viene colorata in rosso, sia se si tratta di un eccesso, sia se si tratta di un deficit.

Cliccando ripetutamente sul pulsante refresh, avete modo di rendervi conto da soli quante volte si verifica che almeno una delle colonne mostra una deviazione significativa. Non si tratta affatto di qualcosa che avviene raramente, perché capita mediamente un po' meno di una volta su 10.

La cosa divertente è che Ruscelli non ha sbagliato solo questa statistica, ma praticamente tutte le sue statistiche nel corso degli ultimi quarant'anni. Perché commette sempre questo stesso errore che lo porta a sovrastimare la significatività statistica, e quindi a trovare delle correlazioni astrologiche quando queste in realtà non ci sono.

Ecco spiegata la differenza che trova nelle sue statistiche basate sul sesso.

Se per gli uomini risulta significativa una fase, e per le donne un'altra, è perché gli eccessi che riscontra nell'una e nell'altra statistica sono casuali.

Ma voi avete mai sentito che Giove in X casa è favorevole per la carriera degli uomini, mentre per le donne la casa favorevole al successo è la quinta?

Io non ho mai notato delle differenze basate sul sesso, con l'astrologia si legge l'anima delle persone, e le anime non hanno sesso.

Certo, ci sono alcune differenze basate sul sesso. Ad esempio una donna che ha molti partner sessuali, di solito non viene giudicata positivamente, al contrario di quello che succede per un uomo. Ma queste differenze che si riscontrano nei due sessi, sono di tipo adattativo, non sono delle differenze sostanziali.

E' giusto interpretare una carta del cielo tenendo conto del sesso di una persona, ma l'influsso astrologico in se, è indipendente dal sesso.

Un errore imperdonabile

Nella tabella qui sopra ci sono i risultati ottenuti da Gabriele Ruscelli in una statistica pubblicata sul numero 183 di Linguaggio Astrale (estate 2016). In pratica con questa sua ricerca Ruscelli intendeva verificare se i politici vincono più frequentemente le elezioni durante una delle 10 fasi del loro personale ciclo sinodico di Giove.

L'ipotesi di partenza
Esiste almeno una fase del ciclo sinodico di Giove durante la quale si verifica un frequenza significativamente elevata di elezioni politiche, per i politici di entrambi i sessi, calcolando il periodo sinodico a partire dalla data di nascita del politico.

Già su questa ipotesi ci sarebbe qualcosa da obiettare. Se Ruscelli crede che esista una relazione tra il ciclo di Giove e le vittorie elettorali, dovrebbe chiedersi se i risultati da lui ottenuti si discostano nel loro insieme da quelli che sono i risultati prevedibili, e se lo fanno in modo statisticamente significativo.

Non si capisce perché parli di frequenza significativamente elevata, visto che una frequenza significativamente bassa, avrebbe comunque la capacità di farci sospettare una relazione tra il ciclo di Giove e le vincite elettorali.

Certo, è naturale, di solito l'attenzione si rivolge più verso gli eccessi che verso i deficit. Però bisognerebbe tenere a mente che se esistesse realmente un influsso astrale legato al ciclo di Giove, questo influsso creerebbe tanto degli eccessi che dei deficit. Perché ovviamente i casi in eccesso che si producono per una fase, sono dei casi in deficit di un'altra fase.

Ma come si fa a sapere se i risultati trovati si discostano in modo significativo dai risultati attesi?

Basta inserire i risultati in questo sito di statistiche.

Ma prima di inserire in questo sito i risultati trovati vi suggerirei di inserire questi risultati.

Il sito ci dice che i risultati trovati sono estremamente statisticamente significativi, con una probabilità che questi risultati siano frutto di un caso molto bassa pari a 0,0007, per cui ci sarebbero solo 7 casi su 10.000 che questi risultati siano frutto di un caso. Eppure, nessuna di queste fasi mostra una deviazione significativa se presa singolarmente. Per cui Ruscelli con questi risultati avrebbe detto che la sua ipotesi non si era realizzata, sebbene l'insieme della tabella mostra un probabilissimo effetto astrologico.

In assenza di ipotesi precise, la cosa migliore da fare è quello di valutare la significatività statistica generale della tabella ottenuta.

Adesso provate ad inserire i risultati realmente ottenuti nel sito e leggete il responso.

Il responso è che le deviazioni trovate per questa tabella non sono significative, perché ci sono circa 12 probabilità su 100 di ottenere delle deviazioni come queste, o maggiori di queste, per un semplice caso.

Naturalmente io non posso imporre la mia ipotesi a Ruscelli, anche se trovo la sua ipotesi poco razionale.

L'ipotesi di Ruscelli in realtà si verifica. Nella fase n.1 della tabella in alto ci sono 278 vittorie mentre il numero atteso era di 234 vittorie.

Ma come si fa a sapere se questo risultato è significativo, e quanto è significativo?

Lo si può sapere utilizzando sempre lo stesso sito. Inserendo i dati della fase n.1 , e quindi 278 come numero trovato e 234 come numero atteso, e creando una nuova categoria che comprende tutti gli altri risultati.

Per cui il numero trovato per questa nuova categoria è dato dal numero totale delle vittorie meno quelle del settore n.1, e il numero atteso è 234 * 9 = 2106.

P value and statistical significance:
Chi squared equals 9.193 with 1 degrees of freedom.
The two-tailed P value equals 0.0024
By conventional criteria, this difference is considered to be very statistically significant.

Per cui il sito ci conferma che quella riscontrata per la fase n.1 è una deviazione significativa e che ci sarebbero solo 2 probabilità su 1000 che questo si sia verificato per caso. Ruscelli, chissà perché, calcola una probabilità leggermente diversa, perché dice che ci sarebbero 4 probabilità su 1000 che questa deviazione si sia verificata per un puro caso. Questa discrepanza non è molto importante, perché comunque l'ordine di grandezza è lo stesso, e se la probabilità è di 2 casi su 1000 o di 4 casi su 1000, non cambia molto.

Ma a cosa si riferisce questa probabilità?

Questa è la probabilità che nella fase n.1 si verificasse una simile deviazione.

Non è la probabilità corrispondente all'ipotesi di Ruscelli.

L'ipotesi di Ruscelli era che almeno per una fase, delle 10 fasi, avrebbe trovato un risultato significativo,
come in effetti è poi avvenuto. Ma la probabilità di questo evento non è quella relativa alla fase n.1.

Questa probabilità andrebbe presa in considerazione se Ruscelli avesse ipotizzato che avrebbe trovato una deviazione importante proprio per questa fase.

Ma l'ipotesi di Ruscelli era generica, non riguardava in modo specifico questa fase n.1, ma coinvolgeva tutte e 10 le fasi che potenzialmente potevano mostrare una deviazione significativa come questa.

In altre parole, se Ruscelli invece di trovare 278 vittorie per la fase n.1, le avesse trovate per la fase n.3 o per la fase n.5, lui sarebbe comunque andato alla cassa per reclamare la sua vincita, perché lui ha scommesso su tutte e 10 le fasi, e non su una fase in particolare.

E quindi qual è la vera probabilità associata all'ipotesi di Ruscelli?

E' molto semplice, è 10 volte la probabilità della fase n.1.

Per cui, è vero che l'ipotesi di Ruscelli si sia verificata, ma la probabilità che questo sia avvenuto per un semplice caso è di 2 casi su 100 e non di 2 casi su 1000.

Per cui la significatività trovata è piuttosto bassa raggiungendo soltanto il livello del 5%.

Immaginate di andare a giocare alla roulette e di puntare 10 euro su un certo numero.
La probabilità di vincita è di 1/37 e se il vostro numero esce il banco vi paga 360 euro.

Se invece puntate 1 euro su 10 numeri diversi, la vostra probabilità di vittoria è di 10/37, e
se uno di questi numeri esce il banco vi da 36 euro, perché su quel numero avete puntato solo un euro.

Ruscelli punta su 10 numeri, e uno di questi effettivamente esce, però non può pretendere una vincita di 360 euro perché gliene spettano solo 36, perché lui avevo distribuito la sua puntata su 10 numeri diversi, e non aveva puntato tutto il suo capitale sull''unico numero che poi è uscito.

Si tratta di logica elementare, e non capisco come ci sia qualcuno che non comprende queste cose.

Il P-Value della somiglianza

Dati Voas

Dati Voas

Ho aggiustato la tabella in modo che ci sia piena corrispondenza con il grafico delle deviazioni riportato in alto. In pratica ho solo invertito le colonne all'interno dei cinque aspetti doppi. Inoltre questa volta ho inserito nella tabella anche i totali delle singole colonne.

I totali delle colonne che appartengono allo stesso aspetto riportano dei risultati che sono molto simili tra loro. La cosa si vede anche ad occhio, le deviazioni per lo stesso aspetto sono molto simili tra loro. Le deviazioni colorate in rosa in cui il segno del marito precede quello della moglie sono molto simili a quelle colorate in verde in cui il segno del marito segue quello delle mogli.

Se prendiamo i 10 valori dei 5 aspetti doppi, e li disegniamo su una linea orizzontale che va da -33 a + 30, diventa chiaro che il modo in cui sono accoppiati questi valori, è uno dei modi migliori in cui potrebbero essere accoppiati.

Supponiamo di non essere in grado di stabilire la significatività statistica delle singole colonne, che poi in parte è vero, perché riesco a calcolare il P-Value di questo tipo di deviazioni solo in modo approssimativo.

Notiamo che ci sono delle deviazioni che vanno da -33 a + 30, ma non sappiamo dire se queste deviazioni siano significative oppure no. Possiamo però calcolare il P-Value della somiglianza tra le colonne dello stesso aspetto.

Questa somiglianza tra le colonne dello stesso aspetto, è importante perché è anch'essa una dimostrazione che i valori riportati nella tavola n.8 di Voas non sono affatto casuali.

Questo P-Value, ad una coda,  è uguale a P = 0,005 e questo significa che avevamo solo 1 probabilità su 200 che si verificasse una somiglianza tra le colonne dello stesso aspetto uguale o maggiore di quella riscontrata. Per cui è piuttosto probabile che questa somiglianza non sia l'effetto di un caso, e che i totali di ciascuna colonna assomiglino a quelli della colonna dello stesso aspetto, perché è proprio l'aspetto che produce quel tipo di deviazione.

Era così difficile?

12 Aspetti

7 Aspetti

Qui abbiamo preso i valori della tavola n.8 di Voas, e abbiamo creato due nuove tabelle dove le coppie sono raggruppate secondo l'aspetto formato dai segni di nascita dei coniugi.

Le deviazioni riscontrate per gli aspetti sono estremamente significative.

Quei numeri che si leggono nell'ultima riga della seconda tavola non potrebbero essere così alti se si trattasse di deviazioni casuali. In particolare sono molto significativi i deficit che si riscontrano per le coppie in quadratura e in quinconce.

Nonostante Voas abbia eliminato l'eccesso delle coppie in congiunzione, non è riuscito ad eliminare il deficit delle coppie in quadratura e in quinconce.

Le coppie in quadratura e in quinconce sono molto meno di quelle che dovrebbero essere, per cui possiamo concludere che c'è qualcosa che fa si che le persone i cui segni formano questi aspetti tendono a sposarsi meno frequentemente del previsto.