Ruscelli vs Ruscelli

Statistica Sportivi

Statistica Politici

L'immagine in alto è stata presa da questa copia di Linguaggio Astrale a pagina 131.

Come si può osservare in questa statistica riguardante gli sportivi Ruscelli calcola la probabilità complessiva della tabella, ottenendo un valore molto basso 0,00001. Per cui ci sarebbe stata solo 1 probabilità su 100.000 di ottenere delle deviazioni come quelle trovate o maggiori di esse, per un semplice caso.

La tabella riportata in alto è molto significativa, per cui se avessimo modo di controllare come sono stati ottenuti questi numeri, potremmo concludere che le vittorie degli sportivi sono legate al loro personale ciclo sinodico di Marte.

Ma come mai questo calcolo della probabilità complessiva non viene fatto per la statistica sui politici?

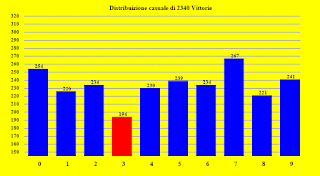
Il primo grafico dimostra che Ruscelli sapeva benissimo che in questo tipo di statistiche bisogna per prima cosa calcolare la probabilità complessiva delle deviazioni riscontrate nella tabella. Ma allora come mai si è dimenticato di applicare questa regola nella statistica sui politici?

La probabilità complessiva della statistica sui politici l'ho calcolata io, come spiegato nei post precedenti, ed è uguale a 0,12 Per cui ci sarebbero state ben 12 probabilità su 100 di ottenere delle deviazioni come quelle trovate o maggiori di esse, per un semplice caso.

Quindi i risultati per i politici non sono per nulla significativi, a differenza di quelli per gli sportivi che erano invece estremamente significativi.

Perché Ruscelli omette di dirci queste cose?

Perché adottare un metodo per una statistica, e un altro metodo per un'altra statistica del tutto uguale alla prima? L'unica differenza tra le due statistiche è che in una si parla di vittorie sportive, e nell'altra di vittorie politiche. 

Il motivo di questo comportamento è molto evidente, a Ruscelli quella probabilità dello 0,12 non piace proprio, perché dimostra la non significatività della sua statistica sui politici, e decide quindi di far sparire questo risultato dalla sua statistica.

Ruscelli scarta i risultati che non gli piacciono.

Una probabilità dello 0,00001 gli piace, e quindi la cita, una probabilità dello 0,12 non gli piace, e quindi non la cita.

Ma se Ruscelli riesce a fare una selezione sui metodi della statistica, applicando di volta in volta i criteri che gli piacciono di più, riuscite ad immaginare che cosa potrebbe combinare nella fase della raccolta dei dati?

Ci vuole veramente poco per alterare i risultati di una statistica, basta eliminare qualche risultato sgradito a favore di qualche risultato gradito.

Motivo per cui non bisogna credere nemmeno nella sua statistica sugli sportivi, anche se in quel caso i numeri sarebbero altamente significativi. 

Ruscelli non riesce ad essere obiettivo, altrimenti non avrebbe omesso di dirci che la tabella delle vittorie dei politici non era significativa.

Io credo che questa manifesta mancanza di oggettività abbia riguardato anche la fase di raccolta dei dati.

Dati, che chissà perché, Ruscelli non vuole mostrare a nessuno.

E i dati?

Questi qui sopra sono dei dati prelevati dall'archivio Gauquelin e che gli sono serviti per elaborare le sue statistiche. Ma dove sono i dati delle statistiche di Ruscelli?

In passato ho richiesto a Ruscelli di poter consultare i dati che gli erano serviti per una sua altra statistica.

Lui prima mi ha raccontato una balla, dicendomi che usava un vecchio software risalente agli anni ottanta, che effettuava i calcoli richiesti, ma che non era in grado di generare una lista dei dati utilizzati nella statistica. Successivamente ha cambiato versione, e mi ha detto che lui a me i suoi dati non me li voleva proprio dare.

Anche in quella occasione motivò il suo rifiuto con una mia presunta indegnità. Se lui non mi dava i suoi dati, la colpa era mia, perché non ero meritevole di riceverli.

Ma non è così che funziona, se si fa una ricerca i dati vanno pubblicati, in modo che chiunque ne fosse interessato possa consultarli, e eventualmente trovarvi degli errori.

Certo, evitando di pubblicare i dati, ci si mette al riparo delle critiche, però così facendo la statistica cessa di essere un lavoro scientifico.

Perché Ruscelli si rifiuta di mostrare i dati che utilizza nelle sue statistiche?

Non gli si richiede di fare un lavoro in più di quello che ha già fatto. 

Se è vero che ha fatto questa ricerca, lui deve avere una lista contenente i nomi dei politici, le loro date di nascita, le date in cui hanno vinto le elezioni, e la fase gioviana corrispondente a ciascuna vittoria elettorale.

Perché Michel Gauquelin riteneva che fosse giusto pubblicare i dati delle sue statistiche, e Gabriele Ruscelli no?

La differenza è data dal fatto che Michel Gauquelin era un ricercatore statistico, e Gabriele Ruscelli no.

Ruscelli è un professorino di chimica di un istituto tecnico, che si illude di aver fatto delle importanti scoperte. Probabilmente queste illusioni gli servono per vivere, magari di se stesso pensa di essere uno scienziato incompreso. Forse pubblicando a raffica queste pseudo statistiche su L.A. spera di pubblicizzare il suo libro di astrologia medica, anche se questo non gli da un vero guadagno, ma solo la soddisfazione di sapere che c'è qualcuno interessato alle sue teorie. 

Se qualcuno prova a chiedergli i dati delle sue statistiche, lui poverino si offende, e dice: "Perché mi chiedi quei dati? Ma allora dubiti della correttezza dei miei calcoli? Pensi che io possa aver imbrogliato? Mi stai offendendo."

Le statistiche di Ruscelli non valgono nulla. 

  

Pacchetto da 10

Non mi date soddisfazione. Finora non c'è stato ancora un blogger che abbia scritto di aver compreso in che consiste l'errore di Ruscelli. Eppure non mi sembra una cosa tanto complicata.

Ho creato una nuova pagina, dove invece che una simulazione alla volta, ne vengono proposte 10 tutte assieme.

Di solito, caricando o ricaricando questa pagina dovreste vedere 1 fase colorata in rosso, anche se qualche volta può capitare che non ne vediate alcuna, così come può capitare che ne vediate più di una.

Le fasce sono colorate in rosso quando mostrano una significatività dello 1%.

Una significatività dello 1% significa che ci aspettiamo di trovare una deviazione del genere circa 1 volta su 100.

Ma allora come mai in questo pacchetto di 10 simulazioni, molto spesso riscontriamo che c'è una fase in rosso? Non dovremmo trovare una fase in rosso, ogni 100 simulazioni? Perché di solito ne bastano solo 10 perché spunti da qualche parte una fascia colorata in rosso?

La risposta è molto semplice. La significatività dello 1%, riguarda quella specifica fascia colorata in rosso.

Se ad esempio la fascia colorata in rosso è la n.1, questo significa che la fascia n.1 sarà colorata in rosso circa 1 volta su 100.

Ma la probabilità di trovare una fascia qualsiasi delle 10, colorata in rosso è 10 volte quella della fascia n.1.

Il pacchetto di 10 simulazioni che vi ho proposto in questa pagina, contiene 100 fasce, per cui è normale che su 100 fasce ce ne sia 1 che risulti significativa al livello dello 1%. Perché è proprio questo quello che ci aspettiamo.

Per cui su 10 simulazioni, ci aspettiamo che ci sia una fascia colorata in rosso.

Bisogna tener presente che siccome stiamo parlando di simulazioni, il risultato di queste simulazioni non potrà mai essere significativo, per cui si parla sempre di falsi positivi, che sembrano indicare come favorevole ora una fascia, ora un'altra.

Visto che ogni 10 simulazioni si presenta un falso positivo, se troviamo nella realtà una fascia significativa allo 1%, non abbiamo motivo di credere che non sia l'effetto di un caso. E comunque la probabilità che questo si verifichi è del 10% e non dello 1%.

Il Ciclo Sinodico di Giove

A quanto pare, nonostante le mie spiegazioni, questa storia della statistica non è ben chiara a tutti. Penso che non sia giusto scannarsi per questo, o prendere una posizione a favore di una tesi o dell'altra, sulla base delle proprie antipatie o simpatie. Non è necessario fare così, perché con un po' di impegno, tutti possono capire di cosa si sta parlando, anche senza essere degli esperti di matematica e statistica.

Ruscelli ha fatto una statistica in cui ipotizza che ci possa essere una relazione tra il ciclo sinodico di Giove e le vittorie elettorali dei politici uomini e dei politici donne analizzati separatamente.

Non è il caso di spiegare in dettaglio che cosa sia questo ciclo sinodico di Giove. Per sommi capi, siccome la Terra compie una rivoluzione intorno al Sole in un anno, e siccome Giove nello stesso tempo percorre circa un segno zodiacale, tra una congiunzione Sole-Giove e quella successiva passano circa 13 mesi. Perché la Terra impiega un anno per tornare nella stessa posizione in cui si trovava un anno prima, e circa un altro mese per raggiungere Giove che nel frattempo si è spostato ed è avanzato di un segno.

Ruscelli nella sua relazione scrive che la durata media di questo periodo è di 398,88 giorni. Non ho controllato questo dato, perché mi fido.

Ognuno di noi nasce in un certo momento del ciclo Sole-Giove, c'è chi nasce durante la congiunzione, c'è chi nasce durante l'opposizione, e in qualsiasi altra fase.

Il ciclo sinodico personale di Giove inizia per ciascuno di noi, quando nello zodiaco si riproduce la stessa distanza angolare tra il Sole e Giove che questi due corpi celesti formavano nel giorno in cui siamo nati.
Quando questo avviene entriamo nella nostra personale fase n.0 del ciclo gioviano.

Invece di andare a vedere con le effemeridi alla mano quando si riproduce esattamente lo stesso angolo tra il Sole e Giove che questi due corpi celesti formavano alla nascita, Ruscelli suggerisce un metodo semplificato basato sul periodo medio di 398,88 giorni che intercorre tra una congiunzione e quella successiva.

Lui calcola il numero dei giorni che sono trascorsi dalla nascita di un uomo politico e il giorno in cui ha vinto le elezioni, e divide questo numero per 398,88. Del quoziente così ottenuto, ignora la parte intera, e sofferma la sua attenzione sulla prima cifra dopo la virgola.  La cifra così ottenuta, è la cifra che indica la fase del ciclo gioviano in cui è avvenuta questa vittoria elettorale.

Io trovo questo metodo simpatico. Non so fino a che punto ci possa essere corrispondenza tra le fasi del ciclo gioviano calcolate in questo modo, e quelle che si potrebbero calcolare con un altro metodo, che tenga conto delle effettive posizioni del Sole e di Giove, sia alla nascita, che nel giorno della vittoria elettorale.

In generale l'astronomia non funziona con i valori medi. Il Sole per tornare nella stessa posizione impiega più o meno sempre lo stesso tempo, ma per Giove le cose sono un po' diverse, perché quando è in prossimità del suo perielio si muove più velocemente, mentre quando è vicino al suo afelio si muove più lentamente, e questo potrebbe complicare le cose.

La questione andrebbe approfondita, però al momento questo non ha grande importanza, e comunque il metodo di Ruscelli per definire le fasi gioviane, è fondamentalmente corretto.

La questione importante è un'altra. Le fasi gioviane definite col metodo appena spiegato, hanno un significato astrologico? Esiste realmente una correlazione tra queste fasi del ciclo personale sinodico di Giove e le vittorie elettorali dei politici?

La statistica di Ruscelli ha proprio lo scopo di appurare l'esistenza di questa correlazione.

Per cui dal prossimo post entrerò nel vivo della statistica.
     

Chiederò al CICAP

Ho intenzione di fotocopiare la statistica di Ruscelli e di sottoporla al vaglio del CICAP.

Gli dirò: Gli astrologi sostengono che esiste una relazione tra il ciclo sinodico di Giove e le vittorie elettorali dei politici, e sostengono di averlo dimostrato per mezzo di una statistica. Voi cosa ne pensate? Le cose stanno veramente così?

Gli dirò esattamente così: "Gli astrologi".

Non gli dirò Gabriele Ruscelli sostiene di aver dimostrato un influsso astrologico per mezzo di una statistica, ma gli dirò che a fare questa affermazione sono TUTTI GLI ASTROLOGI.

Perché?

Perché questa statistica è stata pubblicata su Linguaggio Astrale che è la rivista di astrologia più importante esistente oggi in Italia. Che io sappia, nessuno dei lettori di questa rivista ha trovato qualcosa da obiettare su questa statistica, e quindi, evidentemente, TUTTI GLI ASTROLOGI, ne condividono le conclusioni.

Non so se qualcuno del CICAP avrà voglia di commentare questa statistica, può darsi di si, come può darsi di no. Quello che so è che farò le fotocopie della statistica e che chiederò gentilmente a qualcuno del CICAP di esaminarla.

Gabriele Ruscelli ritiene che io sia un maleducato perché mi sono permesso di evidenziare l'errore evidente che essa contiene. Perché dovrebbe essere una questione di maleducazione?

Per criticare le statistiche di Ruscelli occorre l'approvazione della Sacra Rota?

Non ho rispettato l'etichetta?  Ho infranto qualche regola del galateo?

Perché dire che 2 + 2 non fa 5 ma fa 4 dovrebbe essere da maleducati?

Io mi sono limitato a dire che i calcoli statistici presenti in quella relazione sono errati, per il semplice motivo che quei calcoli sono oggettivamente errati.

Non ho attaccato Ruscelli personalmente, non ho parlato di lui, ma della sua statistica.

Lui invece attacca me personalmente, mi da del maleducato, cercando di offendere non solo me, ma anche i miei genitori che si suppone siano quelli che mi avrebbero dovuto impartire una educazione.

Ruscelli non prova nemmeno a contestare le mie critiche, non dice non è come dici tu perché così, così, così.

Lui dice tu non sei degno di una mia risposta, sei un miserabile, quando in realtà è il suo comportamento ad essere da miserabile.

Io me ne frego del tentativo di Ruscelli di lanciarmi della melma addosso. I suoi giudizi hanno lo stesso valore delle sue statistiche, ossia nessuno.

Le sue statistiche sono il riflesso della sua intelligenza, e il suo modo di reagire alle critiche, cercando di delegittimare i suoi interlocutori, è il riflesso della sua mediocrità e della sua vigliaccheria che è il tratto dominante della sua personalità.

Simulazioni statistiche

Clicca sull'immagine

Ho creato una pagina che distribuisce in modo casuale le 2340 vittorie nelle 10 fasi.

Se una di queste fasi è significativa al livello dello 1%, allora viene colorata in rosso, sia se si tratta di un eccesso, sia se si tratta di un deficit.

Cliccando ripetutamente sul pulsante refresh, avete modo di rendervi conto da soli quante volte si verifica che almeno una delle colonne mostra una deviazione significativa. Non si tratta affatto di qualcosa che avviene raramente, perché capita mediamente un po' meno di una volta su 10.

La cosa divertente è che Ruscelli non ha sbagliato solo questa statistica, ma praticamente tutte le sue statistiche nel corso degli ultimi quarant'anni. Perché commette sempre questo stesso errore che lo porta a sovrastimare la significatività statistica, e quindi a trovare delle correlazioni astrologiche quando queste in realtà non ci sono.

Ecco spiegata la differenza che trova nelle sue statistiche basate sul sesso.

Se per gli uomini risulta significativa una fase, e per le donne un'altra, è perché gli eccessi che riscontra nell'una e nell'altra statistica sono casuali.

Ma voi avete mai sentito che Giove in X casa è favorevole per la carriera degli uomini, mentre per le donne la casa favorevole al successo è la quinta?

Io non ho mai notato delle differenze basate sul sesso, con l'astrologia si legge l'anima delle persone, e le anime non hanno sesso.

Certo, ci sono alcune differenze basate sul sesso. Ad esempio una donna che ha molti partner sessuali, di solito non viene giudicata positivamente, al contrario di quello che succede per un uomo. Ma queste differenze che si riscontrano nei due sessi, sono di tipo adattativo, non sono delle differenze sostanziali.

E' giusto interpretare una carta del cielo tenendo conto del sesso di una persona, ma l'influsso astrologico in se, è indipendente dal sesso.

Un errore imperdonabile

Nella tabella qui sopra ci sono i risultati ottenuti da Gabriele Ruscelli in una statistica pubblicata sul numero 183 di Linguaggio Astrale (estate 2016). In pratica con questa sua ricerca Ruscelli intendeva verificare se i politici vincono più frequentemente le elezioni durante una delle 10 fasi del loro personale ciclo sinodico di Giove.

L'ipotesi di partenza
Esiste almeno una fase del ciclo sinodico di Giove durante la quale si verifica un frequenza significativamente elevata di elezioni politiche, per i politici di entrambi i sessi, calcolando il periodo sinodico a partire dalla data di nascita del politico.

Già su questa ipotesi ci sarebbe qualcosa da obiettare. Se Ruscelli crede che esista una relazione tra il ciclo di Giove e le vittorie elettorali, dovrebbe chiedersi se i risultati da lui ottenuti si discostano nel loro insieme da quelli che sono i risultati prevedibili, e se lo fanno in modo statisticamente significativo.

Non si capisce perché parli di frequenza significativamente elevata, visto che una frequenza significativamente bassa, avrebbe comunque la capacità di farci sospettare una relazione tra il ciclo di Giove e le vincite elettorali.

Certo, è naturale, di solito l'attenzione si rivolge più verso gli eccessi che verso i deficit. Però bisognerebbe tenere a mente che se esistesse realmente un influsso astrale legato al ciclo di Giove, questo influsso creerebbe tanto degli eccessi che dei deficit. Perché ovviamente i casi in eccesso che si producono per una fase, sono dei casi in deficit di un'altra fase.

Ma come si fa a sapere se i risultati trovati si discostano in modo significativo dai risultati attesi?

Basta inserire i risultati in questo sito di statistiche.

Ma prima di inserire in questo sito i risultati trovati vi suggerirei di inserire questi risultati.

Il sito ci dice che i risultati trovati sono estremamente statisticamente significativi, con una probabilità che questi risultati siano frutto di un caso molto bassa pari a 0,0007, per cui ci sarebbero solo 7 casi su 10.000 che questi risultati siano frutto di un caso. Eppure, nessuna di queste fasi mostra una deviazione significativa se presa singolarmente. Per cui Ruscelli con questi risultati avrebbe detto che la sua ipotesi non si era realizzata, sebbene l'insieme della tabella mostra un probabilissimo effetto astrologico.

In assenza di ipotesi precise, la cosa migliore da fare è quello di valutare la significatività statistica generale della tabella ottenuta.

Adesso provate ad inserire i risultati realmente ottenuti nel sito e leggete il responso.

Il responso è che le deviazioni trovate per questa tabella non sono significative, perché ci sono circa 12 probabilità su 100 di ottenere delle deviazioni come queste, o maggiori di queste, per un semplice caso.

Naturalmente io non posso imporre la mia ipotesi a Ruscelli, anche se trovo la sua ipotesi poco razionale.

L'ipotesi di Ruscelli in realtà si verifica. Nella fase n.1 della tabella in alto ci sono 278 vittorie mentre il numero atteso era di 234 vittorie.

Ma come si fa a sapere se questo risultato è significativo, e quanto è significativo?

Lo si può sapere utilizzando sempre lo stesso sito. Inserendo i dati della fase n.1 , e quindi 278 come numero trovato e 234 come numero atteso, e creando una nuova categoria che comprende tutti gli altri risultati.

Per cui il numero trovato per questa nuova categoria è dato dal numero totale delle vittorie meno quelle del settore n.1, e il numero atteso è 234 * 9 = 2106.

P value and statistical significance:
Chi squared equals 9.193 with 1 degrees of freedom.
The two-tailed P value equals 0.0024
By conventional criteria, this difference is considered to be very statistically significant.

Per cui il sito ci conferma che quella riscontrata per la fase n.1 è una deviazione significativa e che ci sarebbero solo 2 probabilità su 1000 che questo si sia verificato per caso. Ruscelli, chissà perché, calcola una probabilità leggermente diversa, perché dice che ci sarebbero 4 probabilità su 1000 che questa deviazione si sia verificata per un puro caso. Questa discrepanza non è molto importante, perché comunque l'ordine di grandezza è lo stesso, e se la probabilità è di 2 casi su 1000 o di 4 casi su 1000, non cambia molto.

Ma a cosa si riferisce questa probabilità?

Questa è la probabilità che nella fase n.1 si verificasse una simile deviazione.

Non è la probabilità corrispondente all'ipotesi di Ruscelli.

L'ipotesi di Ruscelli era che almeno per una fase, delle 10 fasi, avrebbe trovato un risultato significativo,
come in effetti è poi avvenuto. Ma la probabilità di questo evento non è quella relativa alla fase n.1.

Questa probabilità andrebbe presa in considerazione se Ruscelli avesse ipotizzato che avrebbe trovato una deviazione importante proprio per questa fase.

Ma l'ipotesi di Ruscelli era generica, non riguardava in modo specifico questa fase n.1, ma coinvolgeva tutte e 10 le fasi che potenzialmente potevano mostrare una deviazione significativa come questa.

In altre parole, se Ruscelli invece di trovare 278 vittorie per la fase n.1, le avesse trovate per la fase n.3 o per la fase n.5, lui sarebbe comunque andato alla cassa per reclamare la sua vincita, perché lui ha scommesso su tutte e 10 le fasi, e non su una fase in particolare.

E quindi qual è la vera probabilità associata all'ipotesi di Ruscelli?

E' molto semplice, è 10 volte la probabilità della fase n.1.

Per cui, è vero che l'ipotesi di Ruscelli si sia verificata, ma la probabilità che questo sia avvenuto per un semplice caso è di 2 casi su 100 e non di 2 casi su 1000.

Per cui la significatività trovata è piuttosto bassa raggiungendo soltanto il livello del 5%.

Immaginate di andare a giocare alla roulette e di puntare 10 euro su un certo numero.
La probabilità di vincita è di 1/37 e se il vostro numero esce il banco vi paga 360 euro.

Se invece puntate 1 euro su 10 numeri diversi, la vostra probabilità di vittoria è di 10/37, e
se uno di questi numeri esce il banco vi da 36 euro, perché su quel numero avete puntato solo un euro.

Ruscelli punta su 10 numeri, e uno di questi effettivamente esce, però non può pretendere una vincita di 360 euro perché gliene spettano solo 36, perché lui avevo distribuito la sua puntata su 10 numeri diversi, e non aveva puntato tutto il suo capitale sull''unico numero che poi è uscito.

Si tratta di logica elementare, e non capisco come ci sia qualcuno che non comprende queste cose.