La fusione fredda secondo Andrea Rossi

Gabriele Ruscelli ha condiviso questo video su Facebook.

Ma non lo sa che si tratta di una bufala?

Qualcuno mi domanderà: "Astromauh, ma come fai a dire che si tratta di una bufala, sei forse un fisico?"

No, non sono uno fisico, però lo so ugualmente, perché mi sono documentato.

Elezioni : Risultati Definitivi

5295 Vittorie Elettorali

Che cosa mostrano questi risultati?

Mostrano che le deviazioni complessive della tabella non sono significative, con un P Value uguale a 0.2354, perché se attribuissimo a caso le vittorie alle varie fasi, circa una volta su quattro troveremmo dei risultati che si discostano dai valori attesi, come, o in misura maggiore, di quanto si sia verificato nella nostra statistica.

Lo stesso era accaduto nella statistica di Ruscelli, perché anche in quel caso le deviazioni complessive non erano significative, solo che lui aveva ignorato questo fatto, per dire che era estremamente significativo l'eccesso che si era verificato per la fase n.1. 

Ruscelli attribuiva all'eccesso da lui riscontrato per la fase n.1 un P Value pari a 0.004, per cui, secondo lui, c'erano solo 4 probabilità su 1000 che quell'eccesso fosse dovuto ad un caso, e quindi riteneva di aver dimostrato che i politici di sesso maschile vincono più spesso le elezioni quando si trovano nella loro fase personale n.1 del ciclo sinodico di Giove.

Nei post precedenti ho cercato di spiegare che questo non era vero, perché Ruscelli non aveva tenuto conto del fatto che le fasi sono 10, ed aveva quindi sovrastimato il valore della significatività statistica relativa al settore n.1.

In seguito però ho visto che sul sito del Senato della Repubblica, ci sono i dati relativi a tutti i senatori eletti dalla nascita della Repubblica Italiana fino ai giorni nostri, ed ho quindi deciso di replicare la statistica

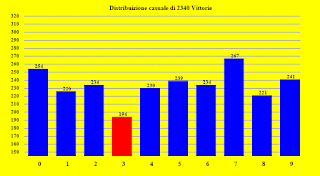
I risultati di questa statistica sono riportati nella tabella in alto, dove si può osservare che le vittorie elettorali relative alla fase n.1 sono 494 mentre il numero atteso per tutte le fasi era 529.5.

E quindi, nella mia statistica, fatta utilizzando i dati ufficiali del Senato della Repubblica, i risultati relativi alla fase n.1 sono addirittura meno di quelli previsti, mentre Ruscelli avrebbe giurato il contrario, perché era convinto di aver scoperto una legge astrologica secondo cui i politici vincono più spesso le elezioni quando sono nella loro fase n.1.

Per cui qui abbiamo una doppia smentita di ciò che Ruscelli pensava di aver dimostrato.

La prima era di carattere teorico, perché ho mostrato che il calcolo della significatività statistica di Ruscelli non teneva conto del fatto che le fasi sono 10, la seconda smentita è invece di carattere pratico e viene dalla mia statistica su un numero di vittorie elettorali che è più del doppio di quelle analizzate da Ruscelli.

A questo punto credo che sarebbe doveroso da parte di Dante Valente che è il direttore responsabile di Linguaggio Astrale, pubblicare un mio articolo sulla rivista in cui spiego perché la statistica di Ruscelli non è valida, e come i suoi risultati siano stati smentiti dalla mia statistica. 

Capisco che possa essere imbarazzante pubblicare una ricerca che ne smentisce un'altra pubblicata nel numero precedente di una rivista astrologica, però questa è una scelta obbligata se si ama l'astrologia.

Oppure preferite applicare le regola "scoperta" da Ruscelli per pronosticare i risultati elettorali dei prossimi cinquant'anni?

Probabilmente potreste preferire questa nuova versione della stessa pagina, in cui vengono mostrati i dettagli del calcolo della fase.

5295 Vittorie Elettorali

Tutto Giusto!

Nell’articolo che ho pubblicato sul n°153 di questa rivista, intitolato “ I segni
zodiacali degli sportivi “, ho affermato che alcuni sostenitori dell’astrologia
hanno effettuato in passato alcune ricerche che sono state condotte con metodologie rigorose e che hanno portato a risultati molto interessanti.
Però, purtroppo, bisogna ammettere che le loro conclusioni non possono
essere ritenute accettabili dal punto di vista scientifico, poiché non sono state
replicate da altri ricercatori.
Gli astrologi infatti hanno la pessima abitudine di non replicare mai le ricerche
dei loro colleghi.
Questo perché dimenticano, ignorano, oppure non vogliono applicare il “
Principio di falsificazione”.
Questo principio è una norma fondamentale del metodo scientifico ed è
stato elaborato dal filosofo britannico di origina austriaca Karl Raimund Popper
(1902 – 1994). Tale criterio afferma che possiamo ritenere attendibile il risultato
di una ricerca o un’ipotesi o una teoria solo quando ha resistito a numerosi
e rigorosi tentativi di confutazione.
È molto importante sottolineare che solo applicando questo principio è possibile
far progredire l’astrologia.
Questa è l’unica strada che dobbiamo percorrere se vogliamo finalmente
trasformare la nostra disciplina in una vera scienza.

Gabriele Ruscelli
(continua a leggere qui a pag.121)

Nulla di Nulla

Visualizza i dati

Ho raccolto finora i dati di 3046 vittorie elettorali, relativi alle legislature dalla VII alla XVII.

Dell'effetto ipotizzato da Ruscelli non vi è alcuna traccia. I politici maschi eletti durante la loro fase n.1 sono 293 e quindi meno del numero previsto 304.6 (un decimo di 3046).

Inoltre i dati contenuti nella tabella non sono significativi nel loro complesso. Ieri avevo calcolato la significatività complessiva della tabella, ma non ricordo bene quale fosse il risultato, mi pare che fosse del 44%.

Provate a calcolarla voi stessi su questo sito.

Questi risultati non sono per nulla significativi.

Qualcuno potrebbe notare che gli eletti della fase n.0 sono sensibilmente maggiori del numero atteso, 339 invece di 304.6. Ma per prima cosa, il settore n.0 non è il settore n.1 che era stato individuato da Ruscelli.

Inserendo i risultati relativi alla fase n.0 nella mia pagina che calcola la significatività, arrotondando il numero atteso a 305 perché la pagina non accetta valori decimali, si scopre che questo risultato sarebbe significativo al livello del 5%, il livello più basso di significatività statistica.

Ma questo avrebbe valore solo se avessimo scommesso su questa specifica fase, invece questa scommessa non l'abbiamo fatta, e avevamo scommesso sulla fase n.1. 

Per cui il valore della probabilità che si legge nell'immagine va moltiplicato per 10, essendo 10 le fasi in cui avremmo potuto riscontrare una deviazione del genere. Per cui c'erano 43 probabilità su 100 che almeno uno dei 10 settori mostrasse una deviazione del genere.

E quindi, in questi risultati non c'è proprio nulla che faccia pensare ad una correlazione tra le vittorie politiche, e le fasi del ciclo sinodico di Giove.

Si è trattato di un miraggio.

Debbo continuare?

Debbo continuare a raccogliere dati?
E' un lavoro così scocciante! Certo ci saranno lavori molto più alienanti e faticosi, come ad esempio la raccolta dei pomodori. Ma quelli che raccolgono i pomodori almeno vengono pagati, quale sarà invece la ricompensa del mio lavoro?

Sulle riviste di astrologia come Linguaggio Astrale vengono riportati lavori e ricerche che sembrano confermare l'astrologia, ma non mi pare di aver mai letto su una rivista astrologica qualche ricerca che smentisce qualche affermazione astrologica.

Non c'è gloria per chi smentisce le affermazioni astrologiche di altri, e anzi chi lo fa nell'ambiente viene considerato uno scostumato. Gli unici autorizzati a smentire delle teorie astrologiche sono solo quelli del CICAP, così noi astrologi possiamo sempre dire che le loro conclusioni non valgono, perché sono travisate dal loro pregiudizio e ignoranza nei confronti dell'astrologia. Ma un astrologo può criticare le teorie di un altro astrologo senza essere giudicato come un traditore?

Eppure gli astrologi sanno benissimo che non tutta l'astrologia è veritiera. Ad esempio, credo che siano in pochi a credere che chi è nato di martedì è combattivo perché è nato nel giorno di Marte, però d'altra parte nessuno si è mai preoccupato di smentire questa cosa, per cui questa affermazione astrologica ha lo stesso valore, che hanno anche tutte le altre affermazioni astrologiche, giuste o sbagliate che siano.

Nuovi Risultati

Nuovi Risultati

Ho raccolto i dati di 2375 vittorie elettorali dei senatori di tutte le legislazioni dalla decima alla diciassettesima. Questi risultati non li ritengo definitivi, perché dovrei controllare meglio alcune cose. Ad esempio, nella decima legislazione in nome di Spadolini, e di un altro senatore, sono ripetuti due volte nel sito senato.it, e per il momento li ho lasciati così. E poi dovrei verificare meglio se il conteggio dei giorni trascorsi dalla nascita al giorno delle elezioni è sempre corretto. Inizialmente pensavo di calcolare questa differenza calcolando il giorno giuliano per entrambe le date, ma poi mi sono accorto che questo non è necessario, perché c'è già una funzione che fa questo calcolo nel linguaggio di programmazione che uso. Ma non mi fido al 100% di questo calcolo, perché è già successo che Microsoft si sia sbagliata su questo. Questo comando legge le date scritte normalmente nella maniera europea (giorno,mese,anno) senza che io abbia specificato da nessuna parte che si tratta di date di questo tipo. Probabilmente fa così perché il server del mio sito è collocato in Italia. Però vorrei controllare un po' meglio tutte queste cose, per cui considerate questi risultati come non definitivi. Fatto sta, che questi risultati non mostrano affatto quanto dichiarato da Ruscelli, perché ci sono 233 vittorie per la fase n.1, ossia meno del valore atteso che è 237.5 (ossia un decimo di 2375). 

Ruscelli pensava di aver dimostrato statisticamente che questa fase del ciclo sinodico personale dei politici favorirebbe le vittorie elettorali, ma stranamente i senatori che sono stati eletti in questa fase del ciclo, nelle ultime otto legislazioni sono addirittura meno della media matematica prevista.

Come si spiega questa cosa?

I miei dati e calcoli sono visibili in rete cliccando sull'immagine in alto, dove sono invece i dati e i calcoli di Ruscelli?

You'd be entitled to think, therefore, that conversion back and forth between PC Excel serial values and Julian day numbers would simply be a matter of adding or subtracting the Julian day number of December 31, 1899 (since the PC Excel days are numbered from 1). But this is a Microsoft calendar, remember, so one must first look to make sure it doesn't contain one of those bonehead blunders characteristic of Microsoft. As is usually the case, one doesn't have to look very far. If you have a copy of PC Excel, fire it up, format a cell as containing a date, and type 60 into it: out pops “February 29, 1900”. News apparently travels very slowly from Rome to Redmond—ever since Pope Gregory revised the calendar in 1582, years divisible by 100 have not been leap years, and consequently the year 1900 contained no February 29th. Due to this morsel of information having been lost somewhere between the Holy See and the Infernal Seattle monopoly, all Excel day numbers for days subsequent to February 28th, 1900 are one day greater than the actual day count from January 1, 1900. Further, note that any computation of the number of days in a period which begins in January or February 1900 and ends in a subsequent month will be off by one—the day count will be one greater than the actual number of days elapsed.

Fourmilab.ch

Risultati Preliminari

Risultati Preliminari

La tabella qui sopra mostra i primi risultati che ho ottenuto riguardanti le vittorie elettorali dei senatori delle ultime quattro legislature (XIV - XV - XVI - XVII).

I valori trovati non si discostano molto da quelli previsti, e le vittorie elettorali della Fase n.1 del ciclo sinodico di Giove, sono leggermente inferiori al numero previsto (111.5).

Naturalmente non voglio confutare la statistica di Ruscelli con una statistica basata su un numero minore di casi, per cui ho intenzione di continuare a raccogliere i dati delle legislature precedenti.

E' un lavoro noiosissimo, perché ci vogliono circa due ore per copiare i dati di una sola legislatura, ma mi sacrificherò per il bene della scienza e dell'astrologia. 

Restano da definire alcune questioni, ad esempio quella dei senatori a vita, che sono inclusi nella lista sebbene non siano stati eletti durante l'elezione in cui sono stati eletti tutti gli altri senatori. Oppure la questione dei subentri quando un politico è chiamato a sostituirne un altro. Non mi è chiaro chi decide chi debba sostituire chi.

Comunque direi che questi problemi non sono tali da invalidare i risultati della statistica, perché la stragrande maggioranza dei senatori sono in queste liste, perché hanno vinto le elezioni.

Per il momento mi dedicherò a copiare i dati dal sito del Senato per rendere il database più consistente.

Io avrei fatto così ...

XVII Legislatura (clicca sull'immagine)

Secondo me la statistica dovrebbe contenere una lista come questa, con il nome e la data di nascita dei politici, e con l'indicazione della fase del ciclo sinodico gioviano di quando hanno vinto le elezioni.

A dire il vero, non ho usato la data delle elezioni, ma quella dell'inizio della legislatura, e quindi uguale per tutti gli eletti della stessa legislatura.

Magari la cosa è discutibile, perché bisognerebbe verificare meglio in che data ciascun senatore ha preso "servizio", perché credo che ce ne siano alcuni che hanno sostituito altri. Oppure bisognerebbe considerare il caso dei senatori a vita, che sono nella lista, pur non essendo stati eletti.

Ma su queste cose si può ragionare soltanto partendo da una lista. Se invece qualcuno si limita a fornire i risultati che ha trovato, non si può sapere come si sia regolato, e quali criteri abbia usato per inserire o non inserire i nominativi nella lista.

Così come non si può controllare se il calcolo delle fasi è corretto.

Ho fatto questa lista di getto, e non ho controllato nulla. Per cui ci potrebbero essere degli errori di trascrizione, e persino nel calcolo delle fasi, perché nemmeno quello ho controllato. 

Non ho intenzione di rifare la statistica di Ruscelli, perché mi annoia copiare tutti i dati. Dovrei ripetere per altre sedici volte il lavoro che ho fatto oggi, e non ne ho voglia. Perché non credo ai risultati di Ruscelli, e lui non ha fatto nulla per invogliarmi a considerare la sua ipotesi.

Forse invece di dichiarare: "Ho trovato questi risultati", bisognerebbe incominciare a mostrare i risultati che si sono trovati. 

Ruscelli vs Ruscelli

Statistica Sportivi

Statistica Politici

L'immagine in alto è stata presa da questa copia di Linguaggio Astrale a pagina 131.

Come si può osservare in questa statistica riguardante gli sportivi Ruscelli calcola la probabilità complessiva della tabella, ottenendo un valore molto basso 0,00001. Per cui ci sarebbe stata solo 1 probabilità su 100.000 di ottenere delle deviazioni come quelle trovate o maggiori di esse, per un semplice caso.

La tabella riportata in alto è molto significativa, per cui se avessimo modo di controllare come sono stati ottenuti questi numeri, potremmo concludere che le vittorie degli sportivi sono legate al loro personale ciclo sinodico di Marte.

Ma come mai questo calcolo della probabilità complessiva non viene fatto per la statistica sui politici?

Il primo grafico dimostra che Ruscelli sapeva benissimo che in questo tipo di statistiche bisogna per prima cosa calcolare la probabilità complessiva delle deviazioni riscontrate nella tabella. Ma allora come mai si è dimenticato di applicare questa regola nella statistica sui politici?

La probabilità complessiva della statistica sui politici l'ho calcolata io, come spiegato nei post precedenti, ed è uguale a 0,12 Per cui ci sarebbero state ben 12 probabilità su 100 di ottenere delle deviazioni come quelle trovate o maggiori di esse, per un semplice caso.

Quindi i risultati per i politici non sono per nulla significativi, a differenza di quelli per gli sportivi che erano invece estremamente significativi.

Perché Ruscelli omette di dirci queste cose?

Perché adottare un metodo per una statistica, e un altro metodo per un'altra statistica del tutto uguale alla prima? L'unica differenza tra le due statistiche è che in una si parla di vittorie sportive, e nell'altra di vittorie politiche. 

Il motivo di questo comportamento è molto evidente, a Ruscelli quella probabilità dello 0,12 non piace proprio, perché dimostra la non significatività della sua statistica sui politici, e decide quindi di far sparire questo risultato dalla sua statistica.

Ruscelli scarta i risultati che non gli piacciono.

Una probabilità dello 0,00001 gli piace, e quindi la cita, una probabilità dello 0,12 non gli piace, e quindi non la cita.

Ma se Ruscelli riesce a fare una selezione sui metodi della statistica, applicando di volta in volta i criteri che gli piacciono di più, riuscite ad immaginare che cosa potrebbe combinare nella fase della raccolta dei dati?

Ci vuole veramente poco per alterare i risultati di una statistica, basta eliminare qualche risultato sgradito a favore di qualche risultato gradito.

Motivo per cui non bisogna credere nemmeno nella sua statistica sugli sportivi, anche se in quel caso i numeri sarebbero altamente significativi. 

Ruscelli non riesce ad essere obiettivo, altrimenti non avrebbe omesso di dirci che la tabella delle vittorie dei politici non era significativa.

Io credo che questa manifesta mancanza di oggettività abbia riguardato anche la fase di raccolta dei dati.

Dati, che chissà perché, Ruscelli non vuole mostrare a nessuno.

E i dati?

Questi qui sopra sono dei dati prelevati dall'archivio Gauquelin e che gli sono serviti per elaborare le sue statistiche. Ma dove sono i dati delle statistiche di Ruscelli?

In passato ho richiesto a Ruscelli di poter consultare i dati che gli erano serviti per una sua altra statistica.

Lui prima mi ha raccontato una balla, dicendomi che usava un vecchio software risalente agli anni ottanta, che effettuava i calcoli richiesti, ma che non era in grado di generare una lista dei dati utilizzati nella statistica. Successivamente ha cambiato versione, e mi ha detto che lui a me i suoi dati non me li voleva proprio dare.

Anche in quella occasione motivò il suo rifiuto con una mia presunta indegnità. Se lui non mi dava i suoi dati, la colpa era mia, perché non ero meritevole di riceverli.

Ma non è così che funziona, se si fa una ricerca i dati vanno pubblicati, in modo che chiunque ne fosse interessato possa consultarli, e eventualmente trovarvi degli errori.

Certo, evitando di pubblicare i dati, ci si mette al riparo delle critiche, però così facendo la statistica cessa di essere un lavoro scientifico.

Perché Ruscelli si rifiuta di mostrare i dati che utilizza nelle sue statistiche?

Non gli si richiede di fare un lavoro in più di quello che ha già fatto. 

Se è vero che ha fatto questa ricerca, lui deve avere una lista contenente i nomi dei politici, le loro date di nascita, le date in cui hanno vinto le elezioni, e la fase gioviana corrispondente a ciascuna vittoria elettorale.

Perché Michel Gauquelin riteneva che fosse giusto pubblicare i dati delle sue statistiche, e Gabriele Ruscelli no?

La differenza è data dal fatto che Michel Gauquelin era un ricercatore statistico, e Gabriele Ruscelli no.

Ruscelli è un professorino di chimica di un istituto tecnico, che si illude di aver fatto delle importanti scoperte. Probabilmente queste illusioni gli servono per vivere, magari di se stesso pensa di essere uno scienziato incompreso. Forse pubblicando a raffica queste pseudo statistiche su L.A. spera di pubblicizzare il suo libro di astrologia medica, anche se questo non gli da un vero guadagno, ma solo la soddisfazione di sapere che c'è qualcuno interessato alle sue teorie. 

Se qualcuno prova a chiedergli i dati delle sue statistiche, lui poverino si offende, e dice: "Perché mi chiedi quei dati? Ma allora dubiti della correttezza dei miei calcoli? Pensi che io possa aver imbrogliato? Mi stai offendendo."

Le statistiche di Ruscelli non valgono nulla. 

  

Pacchetto da 10

Non mi date soddisfazione. Finora non c'è stato ancora un blogger che abbia scritto di aver compreso in che consiste l'errore di Ruscelli. Eppure non mi sembra una cosa tanto complicata.

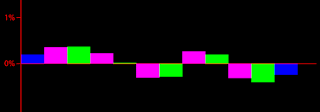
Ho creato una nuova pagina, dove invece che una simulazione alla volta, ne vengono proposte 10 tutte assieme.

Di solito, caricando o ricaricando questa pagina dovreste vedere 1 fase colorata in rosso, anche se qualche volta può capitare che non ne vediate alcuna, così come può capitare che ne vediate più di una.

Le fasce sono colorate in rosso quando mostrano una significatività dello 1%.

Una significatività dello 1% significa che ci aspettiamo di trovare una deviazione del genere circa 1 volta su 100.

Ma allora come mai in questo pacchetto di 10 simulazioni, molto spesso riscontriamo che c'è una fase in rosso? Non dovremmo trovare una fase in rosso, ogni 100 simulazioni? Perché di solito ne bastano solo 10 perché spunti da qualche parte una fascia colorata in rosso?

La risposta è molto semplice. La significatività dello 1%, riguarda quella specifica fascia colorata in rosso.

Se ad esempio la fascia colorata in rosso è la n.1, questo significa che la fascia n.1 sarà colorata in rosso circa 1 volta su 100.

Ma la probabilità di trovare una fascia qualsiasi delle 10, colorata in rosso è 10 volte quella della fascia n.1.

Il pacchetto di 10 simulazioni che vi ho proposto in questa pagina, contiene 100 fasce, per cui è normale che su 100 fasce ce ne sia 1 che risulti significativa al livello dello 1%. Perché è proprio questo quello che ci aspettiamo.

Per cui su 10 simulazioni, ci aspettiamo che ci sia una fascia colorata in rosso.

Bisogna tener presente che siccome stiamo parlando di simulazioni, il risultato di queste simulazioni non potrà mai essere significativo, per cui si parla sempre di falsi positivi, che sembrano indicare come favorevole ora una fascia, ora un'altra.

Visto che ogni 10 simulazioni si presenta un falso positivo, se troviamo nella realtà una fascia significativa allo 1%, non abbiamo motivo di credere che non sia l'effetto di un caso. E comunque la probabilità che questo si verifichi è del 10% e non dello 1%.

Il Ciclo Sinodico di Giove

A quanto pare, nonostante le mie spiegazioni, questa storia della statistica non è ben chiara a tutti. Penso che non sia giusto scannarsi per questo, o prendere una posizione a favore di una tesi o dell'altra, sulla base delle proprie antipatie o simpatie. Non è necessario fare così, perché con un po' di impegno, tutti possono capire di cosa si sta parlando, anche senza essere degli esperti di matematica e statistica.

Ruscelli ha fatto una statistica in cui ipotizza che ci possa essere una relazione tra il ciclo sinodico di Giove e le vittorie elettorali dei politici uomini e dei politici donne analizzati separatamente.

Non è il caso di spiegare in dettaglio che cosa sia questo ciclo sinodico di Giove. Per sommi capi, siccome la Terra compie una rivoluzione intorno al Sole in un anno, e siccome Giove nello stesso tempo percorre circa un segno zodiacale, tra una congiunzione Sole-Giove e quella successiva passano circa 13 mesi. Perché la Terra impiega un anno per tornare nella stessa posizione in cui si trovava un anno prima, e circa un altro mese per raggiungere Giove che nel frattempo si è spostato ed è avanzato di un segno.

Ruscelli nella sua relazione scrive che la durata media di questo periodo è di 398,88 giorni. Non ho controllato questo dato, perché mi fido.

Ognuno di noi nasce in un certo momento del ciclo Sole-Giove, c'è chi nasce durante la congiunzione, c'è chi nasce durante l'opposizione, e in qualsiasi altra fase.

Il ciclo sinodico personale di Giove inizia per ciascuno di noi, quando nello zodiaco si riproduce la stessa distanza angolare tra il Sole e Giove che questi due corpi celesti formavano nel giorno in cui siamo nati.
Quando questo avviene entriamo nella nostra personale fase n.0 del ciclo gioviano.

Invece di andare a vedere con le effemeridi alla mano quando si riproduce esattamente lo stesso angolo tra il Sole e Giove che questi due corpi celesti formavano alla nascita, Ruscelli suggerisce un metodo semplificato basato sul periodo medio di 398,88 giorni che intercorre tra una congiunzione e quella successiva.

Lui calcola il numero dei giorni che sono trascorsi dalla nascita di un uomo politico e il giorno in cui ha vinto le elezioni, e divide questo numero per 398,88. Del quoziente così ottenuto, ignora la parte intera, e sofferma la sua attenzione sulla prima cifra dopo la virgola.  La cifra così ottenuta, è la cifra che indica la fase del ciclo gioviano in cui è avvenuta questa vittoria elettorale.

Io trovo questo metodo simpatico. Non so fino a che punto ci possa essere corrispondenza tra le fasi del ciclo gioviano calcolate in questo modo, e quelle che si potrebbero calcolare con un altro metodo, che tenga conto delle effettive posizioni del Sole e di Giove, sia alla nascita, che nel giorno della vittoria elettorale.

In generale l'astronomia non funziona con i valori medi. Il Sole per tornare nella stessa posizione impiega più o meno sempre lo stesso tempo, ma per Giove le cose sono un po' diverse, perché quando è in prossimità del suo perielio si muove più velocemente, mentre quando è vicino al suo afelio si muove più lentamente, e questo potrebbe complicare le cose.

La questione andrebbe approfondita, però al momento questo non ha grande importanza, e comunque il metodo di Ruscelli per definire le fasi gioviane, è fondamentalmente corretto.

La questione importante è un'altra. Le fasi gioviane definite col metodo appena spiegato, hanno un significato astrologico? Esiste realmente una correlazione tra queste fasi del ciclo personale sinodico di Giove e le vittorie elettorali dei politici?

La statistica di Ruscelli ha proprio lo scopo di appurare l'esistenza di questa correlazione.

Per cui dal prossimo post entrerò nel vivo della statistica.
     

Chiederò al CICAP

Ho intenzione di fotocopiare la statistica di Ruscelli e di sottoporla al vaglio del CICAP.

Gli dirò: Gli astrologi sostengono che esiste una relazione tra il ciclo sinodico di Giove e le vittorie elettorali dei politici, e sostengono di averlo dimostrato per mezzo di una statistica. Voi cosa ne pensate? Le cose stanno veramente così?

Gli dirò esattamente così: "Gli astrologi".

Non gli dirò Gabriele Ruscelli sostiene di aver dimostrato un influsso astrologico per mezzo di una statistica, ma gli dirò che a fare questa affermazione sono TUTTI GLI ASTROLOGI.

Perché?

Perché questa statistica è stata pubblicata su Linguaggio Astrale che è la rivista di astrologia più importante esistente oggi in Italia. Che io sappia, nessuno dei lettori di questa rivista ha trovato qualcosa da obiettare su questa statistica, e quindi, evidentemente, TUTTI GLI ASTROLOGI, ne condividono le conclusioni.

Non so se qualcuno del CICAP avrà voglia di commentare questa statistica, può darsi di si, come può darsi di no. Quello che so è che farò le fotocopie della statistica e che chiederò gentilmente a qualcuno del CICAP di esaminarla.

Gabriele Ruscelli ritiene che io sia un maleducato perché mi sono permesso di evidenziare l'errore evidente che essa contiene. Perché dovrebbe essere una questione di maleducazione?

Per criticare le statistiche di Ruscelli occorre l'approvazione della Sacra Rota?

Non ho rispettato l'etichetta?  Ho infranto qualche regola del galateo?

Perché dire che 2 + 2 non fa 5 ma fa 4 dovrebbe essere da maleducati?

Io mi sono limitato a dire che i calcoli statistici presenti in quella relazione sono errati, per il semplice motivo che quei calcoli sono oggettivamente errati.

Non ho attaccato Ruscelli personalmente, non ho parlato di lui, ma della sua statistica.

Lui invece attacca me personalmente, mi da del maleducato, cercando di offendere non solo me, ma anche i miei genitori che si suppone siano quelli che mi avrebbero dovuto impartire una educazione.

Ruscelli non prova nemmeno a contestare le mie critiche, non dice non è come dici tu perché così, così, così.

Lui dice tu non sei degno di una mia risposta, sei un miserabile, quando in realtà è il suo comportamento ad essere da miserabile.

Io me ne frego del tentativo di Ruscelli di lanciarmi della melma addosso. I suoi giudizi hanno lo stesso valore delle sue statistiche, ossia nessuno.

Le sue statistiche sono il riflesso della sua intelligenza, e il suo modo di reagire alle critiche, cercando di delegittimare i suoi interlocutori, è il riflesso della sua mediocrità e della sua vigliaccheria che è il tratto dominante della sua personalità.

Simulazioni statistiche

Clicca sull'immagine

Ho creato una pagina che distribuisce in modo casuale le 2340 vittorie nelle 10 fasi.

Se una di queste fasi è significativa al livello dello 1%, allora viene colorata in rosso, sia se si tratta di un eccesso, sia se si tratta di un deficit.

Cliccando ripetutamente sul pulsante refresh, avete modo di rendervi conto da soli quante volte si verifica che almeno una delle colonne mostra una deviazione significativa. Non si tratta affatto di qualcosa che avviene raramente, perché capita mediamente un po' meno di una volta su 10.

La cosa divertente è che Ruscelli non ha sbagliato solo questa statistica, ma praticamente tutte le sue statistiche nel corso degli ultimi quarant'anni. Perché commette sempre questo stesso errore che lo porta a sovrastimare la significatività statistica, e quindi a trovare delle correlazioni astrologiche quando queste in realtà non ci sono.

Ecco spiegata la differenza che trova nelle sue statistiche basate sul sesso.

Se per gli uomini risulta significativa una fase, e per le donne un'altra, è perché gli eccessi che riscontra nell'una e nell'altra statistica sono casuali.

Ma voi avete mai sentito che Giove in X casa è favorevole per la carriera degli uomini, mentre per le donne la casa favorevole al successo è la quinta?

Io non ho mai notato delle differenze basate sul sesso, con l'astrologia si legge l'anima delle persone, e le anime non hanno sesso.

Certo, ci sono alcune differenze basate sul sesso. Ad esempio una donna che ha molti partner sessuali, di solito non viene giudicata positivamente, al contrario di quello che succede per un uomo. Ma queste differenze che si riscontrano nei due sessi, sono di tipo adattativo, non sono delle differenze sostanziali.

E' giusto interpretare una carta del cielo tenendo conto del sesso di una persona, ma l'influsso astrologico in se, è indipendente dal sesso.

Un errore imperdonabile

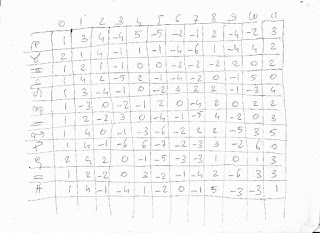
Nella tabella qui sopra ci sono i risultati ottenuti da Gabriele Ruscelli in una statistica pubblicata sul numero 183 di Linguaggio Astrale (estate 2016). In pratica con questa sua ricerca Ruscelli intendeva verificare se i politici vincono più frequentemente le elezioni durante una delle 10 fasi del loro personale ciclo sinodico di Giove.

L'ipotesi di partenza
Esiste almeno una fase del ciclo sinodico di Giove durante la quale si verifica un frequenza significativamente elevata di elezioni politiche, per i politici di entrambi i sessi, calcolando il periodo sinodico a partire dalla data di nascita del politico.

Già su questa ipotesi ci sarebbe qualcosa da obiettare. Se Ruscelli crede che esista una relazione tra il ciclo di Giove e le vittorie elettorali, dovrebbe chiedersi se i risultati da lui ottenuti si discostano nel loro insieme da quelli che sono i risultati prevedibili, e se lo fanno in modo statisticamente significativo.

Non si capisce perché parli di frequenza significativamente elevata, visto che una frequenza significativamente bassa, avrebbe comunque la capacità di farci sospettare una relazione tra il ciclo di Giove e le vincite elettorali.

Certo, è naturale, di solito l'attenzione si rivolge più verso gli eccessi che verso i deficit. Però bisognerebbe tenere a mente che se esistesse realmente un influsso astrale legato al ciclo di Giove, questo influsso creerebbe tanto degli eccessi che dei deficit. Perché ovviamente i casi in eccesso che si producono per una fase, sono dei casi in deficit di un'altra fase.

Ma come si fa a sapere se i risultati trovati si discostano in modo significativo dai risultati attesi?

Basta inserire i risultati in questo sito di statistiche.

Ma prima di inserire in questo sito i risultati trovati vi suggerirei di inserire questi risultati.

Il sito ci dice che i risultati trovati sono estremamente statisticamente significativi, con una probabilità che questi risultati siano frutto di un caso molto bassa pari a 0,0007, per cui ci sarebbero solo 7 casi su 10.000 che questi risultati siano frutto di un caso. Eppure, nessuna di queste fasi mostra una deviazione significativa se presa singolarmente. Per cui Ruscelli con questi risultati avrebbe detto che la sua ipotesi non si era realizzata, sebbene l'insieme della tabella mostra un probabilissimo effetto astrologico.

In assenza di ipotesi precise, la cosa migliore da fare è quello di valutare la significatività statistica generale della tabella ottenuta.

Adesso provate ad inserire i risultati realmente ottenuti nel sito e leggete il responso.

Il responso è che le deviazioni trovate per questa tabella non sono significative, perché ci sono circa 12 probabilità su 100 di ottenere delle deviazioni come queste, o maggiori di queste, per un semplice caso.

Naturalmente io non posso imporre la mia ipotesi a Ruscelli, anche se trovo la sua ipotesi poco razionale.

L'ipotesi di Ruscelli in realtà si verifica. Nella fase n.1 della tabella in alto ci sono 278 vittorie mentre il numero atteso era di 234 vittorie.

Ma come si fa a sapere se questo risultato è significativo, e quanto è significativo?

Lo si può sapere utilizzando sempre lo stesso sito. Inserendo i dati della fase n.1 , e quindi 278 come numero trovato e 234 come numero atteso, e creando una nuova categoria che comprende tutti gli altri risultati.

Per cui il numero trovato per questa nuova categoria è dato dal numero totale delle vittorie meno quelle del settore n.1, e il numero atteso è 234 * 9 = 2106.

P value and statistical significance:
Chi squared equals 9.193 with 1 degrees of freedom.
The two-tailed P value equals 0.0024
By conventional criteria, this difference is considered to be very statistically significant.

Per cui il sito ci conferma che quella riscontrata per la fase n.1 è una deviazione significativa e che ci sarebbero solo 2 probabilità su 1000 che questo si sia verificato per caso. Ruscelli, chissà perché, calcola una probabilità leggermente diversa, perché dice che ci sarebbero 4 probabilità su 1000 che questa deviazione si sia verificata per un puro caso. Questa discrepanza non è molto importante, perché comunque l'ordine di grandezza è lo stesso, e se la probabilità è di 2 casi su 1000 o di 4 casi su 1000, non cambia molto.

Ma a cosa si riferisce questa probabilità?

Questa è la probabilità che nella fase n.1 si verificasse una simile deviazione.

Non è la probabilità corrispondente all'ipotesi di Ruscelli.

L'ipotesi di Ruscelli era che almeno per una fase, delle 10 fasi, avrebbe trovato un risultato significativo,
come in effetti è poi avvenuto. Ma la probabilità di questo evento non è quella relativa alla fase n.1.

Questa probabilità andrebbe presa in considerazione se Ruscelli avesse ipotizzato che avrebbe trovato una deviazione importante proprio per questa fase.

Ma l'ipotesi di Ruscelli era generica, non riguardava in modo specifico questa fase n.1, ma coinvolgeva tutte e 10 le fasi che potenzialmente potevano mostrare una deviazione significativa come questa.

In altre parole, se Ruscelli invece di trovare 278 vittorie per la fase n.1, le avesse trovate per la fase n.3 o per la fase n.5, lui sarebbe comunque andato alla cassa per reclamare la sua vincita, perché lui ha scommesso su tutte e 10 le fasi, e non su una fase in particolare.

E quindi qual è la vera probabilità associata all'ipotesi di Ruscelli?

E' molto semplice, è 10 volte la probabilità della fase n.1.

Per cui, è vero che l'ipotesi di Ruscelli si sia verificata, ma la probabilità che questo sia avvenuto per un semplice caso è di 2 casi su 100 e non di 2 casi su 1000.

Per cui la significatività trovata è piuttosto bassa raggiungendo soltanto il livello del 5%.

Immaginate di andare a giocare alla roulette e di puntare 10 euro su un certo numero.
La probabilità di vincita è di 1/37 e se il vostro numero esce il banco vi paga 360 euro.

Se invece puntate 1 euro su 10 numeri diversi, la vostra probabilità di vittoria è di 10/37, e
se uno di questi numeri esce il banco vi da 36 euro, perché su quel numero avete puntato solo un euro.

Ruscelli punta su 10 numeri, e uno di questi effettivamente esce, però non può pretendere una vincita di 360 euro perché gliene spettano solo 36, perché lui avevo distribuito la sua puntata su 10 numeri diversi, e non aveva puntato tutto il suo capitale sull''unico numero che poi è uscito.

Si tratta di logica elementare, e non capisco come ci sia qualcuno che non comprende queste cose.

Il P-Value della somiglianza

Dati Voas

Dati Voas

Ho aggiustato la tabella in modo che ci sia piena corrispondenza con il grafico delle deviazioni riportato in alto. In pratica ho solo invertito le colonne all'interno dei cinque aspetti doppi. Inoltre questa volta ho inserito nella tabella anche i totali delle singole colonne.

I totali delle colonne che appartengono allo stesso aspetto riportano dei risultati che sono molto simili tra loro. La cosa si vede anche ad occhio, le deviazioni per lo stesso aspetto sono molto simili tra loro. Le deviazioni colorate in rosa in cui il segno del marito precede quello della moglie sono molto simili a quelle colorate in verde in cui il segno del marito segue quello delle mogli.

Se prendiamo i 10 valori dei 5 aspetti doppi, e li disegniamo su una linea orizzontale che va da -33 a + 30, diventa chiaro che il modo in cui sono accoppiati questi valori, è uno dei modi migliori in cui potrebbero essere accoppiati.

Supponiamo di non essere in grado di stabilire la significatività statistica delle singole colonne, che poi in parte è vero, perché riesco a calcolare il P-Value di questo tipo di deviazioni solo in modo approssimativo.

Notiamo che ci sono delle deviazioni che vanno da -33 a + 30, ma non sappiamo dire se queste deviazioni siano significative oppure no. Possiamo però calcolare il P-Value della somiglianza tra le colonne dello stesso aspetto.

Questa somiglianza tra le colonne dello stesso aspetto, è importante perché è anch'essa una dimostrazione che i valori riportati nella tavola n.8 di Voas non sono affatto casuali.

Questo P-Value, ad una coda,  è uguale a P = 0,005 e questo significa che avevamo solo 1 probabilità su 200 che si verificasse una somiglianza tra le colonne dello stesso aspetto uguale o maggiore di quella riscontrata. Per cui è piuttosto probabile che questa somiglianza non sia l'effetto di un caso, e che i totali di ciascuna colonna assomiglino a quelli della colonna dello stesso aspetto, perché è proprio l'aspetto che produce quel tipo di deviazione.

Era così difficile?

12 Aspetti

7 Aspetti

Qui abbiamo preso i valori della tavola n.8 di Voas, e abbiamo creato due nuove tabelle dove le coppie sono raggruppate secondo l'aspetto formato dai segni di nascita dei coniugi.

Le deviazioni riscontrate per gli aspetti sono estremamente significative.

Quei numeri che si leggono nell'ultima riga della seconda tavola non potrebbero essere così alti se si trattasse di deviazioni casuali. In particolare sono molto significativi i deficit che si riscontrano per le coppie in quadratura e in quinconce.

Nonostante Voas abbia eliminato l'eccesso delle coppie in congiunzione, non è riuscito ad eliminare il deficit delle coppie in quadratura e in quinconce.

Le coppie in quadratura e in quinconce sono molto meno di quelle che dovrebbero essere, per cui possiamo concludere che c'è qualcosa che fa si che le persone i cui segni formano questi aspetti tendono a sposarsi meno frequentemente del previsto.

L'intelligenza delle mani

Io ancora disegno gli oroscopi a mano. Se una carta del cielo mi interessa particolarmente faccio i calcoli con il computer, ma poi disegno il grafico a mano. Mi aiuta a concentrarmi, disegnare Marte al 25esimo grado dello Scorpione, è diverso da vedere Marte al 25esimo grado dello Scorpione. E' solo nel momento in cui traccio il simbolo di Marte in un oroscopo, che mi rendo conto che Marte stava proprio lì dove lo disegno, e non da un'altra parte. Ed è solo in questo momento che incomincio a chiedermi  PERCHE' Marte è proprio in quella posizione, e che cosa significa per il consultante.

I simboli dei segni e dei pianeti che disegno a mano, sono diversi da quelli di un grafico computerizzato.

Se non disegno l'oroscopo alla mia maniera, non mi ci trovo, perché non sto utilizzando i miei simboli.

Con il passare degli anni ho modificato il modo di scrivere i segni zodiacali, così come avviene per la scrittura. A scuola si apprende un modello, ma poi ognuno scrive in un modo personale, allontanandosi da questo modello.

Ho riflettuto sul mio modo di scrivere i segni zodiacali, e questo mi ha permesso di capire alcune cose che non avevo ben compreso prima. Il mio modo di disegnare i simboli zodiacali richiama molto gli organi del corpo umano a cui il segno è associato. Ad esempio rappresento il segno del Cancro come un seno, e il segno dello Scorpione come l'organo sessuale maschile a riposo. Il segno del Capricorno lo disegno come un ginocchio, il segno della Bilancia come un paio di reni, il segno dell'Ariete come un cervello, e quello della Vergine come un pugno chiuso.

Comunque credo che i mie segni disegnati a mano siano comprensibilissimi per gli altri astrologi, perché non mi sono allontanato più di tanto dal modello che viene proposto, però io mi accorgo di questa personalizzazione che ho attuato inconsapevolmente, e che mi porta a disegnare delle parti del corpo umano al posto dei simboli classici.

Come se la mia mano avesse capito prima della mia mente, il legame che c'è tra i segni e la fisiologia umana.  

E' per questo che vi chiedevo di disegnare la tabella aspetti. Vi suggerivo di sfruttare l'intelligenza delle vostre stesse mani.

Un conto è se io vi racconto una cosa, ed un altro se la verificate da soli con le vostre mani.

Disegnare a mano questa tabella vi aiuterebbe a capire qualcosa che sarebbe più difficile da capire se ve lo spiegassi.

Esercizio

Tavola n.8

Ordinare i risultati della tavola n.8 di Voas in base agli aspetti, e calcolare i totali di ciascun aspetto.


Un metodo potrebbe essere quello di lasciare invariata la colonna delle wife e cancellare la riga degli husband per sostituirli con 0, 1, 2, 3 ..11.

La prima riga, quella delle donne Ariete si può lasciare così, mentre la seconda riga relativa al Toro deve slittare di un posto. Cioè il risultato che si trova all'incrocio Toro-Toro deve diventare il primo della riga, mentre il risultato che ora è il primo della riga viene scalzato all'ultimo posto.
E poi si procede con lo stesso metodo per le righe successive.

Una volta ottenuta la tavola con 12 aspetti si possono raggruppare insieme gli aspetti simili.

0    Congiunzione

1 e 11 Semisestile

2 e 10 Sestile

3 e 9 Quadratura

4 e 8 Trigono

5 e 7 Quinconce

6   Opposizione

Ottenendo cosi una tavola di sette aspetti dalla congiunzione (0) all'opposizione(6).

Un ordine evidente

Tavola dati Voas

A pagina 12 della voasastrology Voas scrive:

The nature of commissioned table C0792 makes it possible to carry out at least two further types of test. First, one can compare sets of birthdays defined not only by sun sign or month, but on any basis at all. Unless the discrepancies between the actual and expected counts are larger and more systematic when using sun sign rather than other groupings, there is no evidence to support their alleged influence.

Secondly, C0792 provides a full breakdown of spousal dates of birth by age of husband. There are four broad age groups of roughly similar size: under 40, 40-49, 50-64, and 65 and over. Only if the pattern of deviations (as shown in Table 8) is the same in all four groups would it suggest that the discrepancies are non-random.

Qui Voas dice che la tavola da lui commissionata allo ONS, e che contiene il numero dei matrimoni per ciascuna delle 366 x 366 combinazioni del giorno di nascita dei coniugi, ci permette di raggruppare le coppie in modi diversi, e che solo se le deviazioni riscontrate con i segni sono più grandi e più sistematiche di quelle ottenute con altri raggruppamenti, questo sarebbe una prova a favore dell'influsso dei segni.

Poi Voas dice che ha anche quattro sottogruppi della statistica, basati sulle fasce di età dei mariti.
Il fatto di avere i dati raggruppati per età, permetterebbe di confrontare le deviazioni che si riscontrano nei 4 gruppi, e di verificare se queste deviazioni sono simili. Se questo si verificasse, la cosa farebbe pensare che le deviazioni non siano casuali.

Ma Voas non effettua questi test.

Io il primo test l'ho eseguito, ossia ho provato a vedere se invece di considerare i segni zodiacali normali, se ne utilizzano altri fittizi. Ma di questo ne parlerò in seguito.

Per quanto riguarda il secondo test, lui ha i dati divisi anche per fascia di età (dei mariti) ma io non ho questi dati, per cui non potrei fare questo test. Ma ciò che dice è giusto, se le quattro cartelle mostrassero delle deviazioni simili, questo rafforzerebbe molto l'idea di un influsso astrologico.

Quello che non si capisce è perché non applica questo stesso principio ai risultati della statistica complessiva.

Il punto di forza della mia statistica, è dato proprio dal fatto che i segni mostrano tutti un comportamento simile. Gli Ariete, i Toro, i Gemelli ecc. hanno tutti un comportamento simile: Vanno d'accordo con se stessi, e non vanno d'accordo con i segni in quadratura, quinconce, e opposizione.

Prima di pensare alle sue cartelle divise per fasce di età, avrebbe dovuto pensare alla divisione in 12 sottogruppi della cartella principale.

C'è già una suddivisione naturale in 12 sottogruppi nella cartella principale, perché i segni sono 12.
Per cui possiamo andare a vedere che cosa fa l'Ariete con i suoi segni in quadratura, e poi confrontarlo con come si comporta il Toro con i suoi segni in quadratura, e confrontarlo con come si comporta il Gemelli, con i suoi segni in quadratura.

I SEGNI SI COMPORTANO TUTTI NELLA STESSA MANIERA a parte delle piccole variazioni casuali.

Dai dati della statistica possiamo estrapolare una legge a carattere generale, ciascun segno va d'accordo con se stesso, e non va d'accordo con i segni in quadratura, quinconce, e opposizione.

Questa regola ha pochissime eccezioni se si guarda ad uno specifico segno.

Tutto ciò è una ulteriore conferma delle deviazioni trovate, perché la regola generale è confermata dai 12 "sottogruppi", ed è lo stesso Voas a dirci, che quando questo si verifica sia ha la conferma che i risultati non sono random.

Ma veramente ci vorrebbe un esperto?

I dati mostrati nell'immagine qui sopra non sono sufficienti?

Quell'immagine riporta i risultati elaborati da Voas nella sua tavola n.7 e che gli fa concludere che non c'è un influsso dei segni sull'amore.

Io mi sono limitato a "raddrizzare" le diagonali della sua tavola n.7, trasformandole in colonne.

A ciascuna di queste colonne corrisponde quindi un aspetto. L'aspetto 0 è la congiunzione e a seguire abbiamo nell'ordine il semisestile, il sestile, la quadratura, il trigono, il quinconce e l'opposizione.

Il grafico mostra che gli aspetti tendono ad avere un colore predominante, come se ci fosse un influsso che rende favorevole o sfavorevole questo aspetto.

In una distribuzione casuale non dovrebbe essere così, le caselle celesti e le caselle rosse dovrebbero essere sparpagliate alla rinfusa in quella tavola. Al contrario c'è un ordine molto evidente. 

Capire la statistica

La Coppia Lei Leone - Lui Scorpione

L'immagine qui sopra mostra i risultati relativi alla coppia Lei Leone - Lui Scorpione nella mia statistica.

Le coppie Osservate sono state 64.264 mentre le coppie previste erano 64.566, per cui abbiamo trovato 302 coppie in meno del previsto che percentualmente corrispondono allo 0,47% in meno del previsto.

Sulla base di questo risultato possiamo dire che c'è un influsso astrologico che fa si che le coppie Lei Leone - lui Scorpione tendano ad evitare di sposarsi tra loro?

Magari qualche astrologo risponderebbe di si, perché secondo alcuni il solo fatto che esista una differenza tra il numero atteso e il numero previsto è già di per se significativo. Ma si tratterebbe di un errore.

Se io faccio una statistica sui medici e viene fuori che in un database con le date di nascita di un certo numero di medici quelli più numerosi sono i medici del Leone, non posso concludere che il segno del Leone favorisce la professione medica, a meno che quelli del Leone non siano più numerosi del previsto in un modo statisticamente significativo.

Se nella mia statistica il medici del segno del Leone risultano più numerosi del previsto in modo statisticamente significativo questo significa che se ripetessi la statistica con un campione di medici diversi, molto probabilmente troverei che anche in questo nuovo campione i medici del Leone risultano molto più numerosi del previsto .

Se invece nella prima statistica quelli del Leone fossero risultati più del previsto ma non in modo statisticamente significativo, nella seconda statistica ripetuta con soggetti diversi potrei trovare che i medici più numerosi siano del Toro o di qualche altro segno.

Gli astrologi che sono poco ferrati in statistica, tendono a non fare distinzione tra risultati significativi e risultati non significativi, perché non tengono in considerazione l'effetto del caso.

In questa statistica sui medici sicuramente troverò che ci sarà un segno più frequente degli altri, ma avverrebbe lo stesso se estraessi da un contenitore delle palline di ping-pong con i simboli zodiacali disegnati sopra.

In una statistica seria è necessario valutare quello che potrebbe essere una conseguenza del caso, e fortunatamente la scienza statistica ci fornisce gli strumenti matematici per farlo.

Torniamo quindi ai risultati ottenuti con la mia statistica per la coppia Lei Leone - Lui Scorpione.

Nel grafico leggiamo che P = 0,1972 e che il risultato non è statisticamente significativo. Per essere significativo il P-Value dovrebbe essere inferiore a 0,05 e in questo caso non lo è.  

Per cui in pratica il P-Value ci suggerisce di non credere alla deviazione del -0,47% che vediamo in alto.

La deviazione c'è ma dovrebbe dipendere da un caso, perché per caso circa una volta su 5, si ottengono delle deviazioni ancora più grandi di quella trovata.

Per cui, sulla base di questi risultati, dovremmo concludere che non è vero che la coppia Lei Leone-Lui Scorpione sia una coppia poco fortunata. E che si tratta di un tipo di coppia che non mostra alcun tipo di influsso astrologico, perché i risultati trovati non si discostano in modo significativo da quelli previsti.

Ma la coppia Lei Leone-Lui Scorpione è una coppia in quadratura, e come questa ci sono altre 23 coppie in quadratura nello zodiaco.

Proviamo quindi ad analizzare i dati delle 24 coppie in quadratura nel loro insieme.

L'insieme delle Coppie in Quadratura

Il numero di coppie previste è 1.691.856 e quello delle coppie osservate è 1.683.929, per cui ci sono 7927 coppie in meno del previsto. La variazione in termini percentuali è sempre del -0,47% come lo era nel caso della coppia Lei Leone-Lui Scorpione, però in questo caso, è cambiato il P-Value e questa deviazione è estremamente statisticamente significativa.

P = 2,1E-11 significa che ci sono solo due possibilità su 100 miliardi che questa deviazione sia il risultato di un caso. Una sola probabilità su 50 miliardi.

Da 1 probabilità su 5 siamo quindi passati a 1 probabilità su 50 miliardi.

Quali sono le implicazioni per la coppia Lei Leone-Lui Scorpione?

Quella deviazione del -0,47% che ci sembrava poco, o per nulla significativa, in realtà lo è, perché è la deviazione tipica di tutte le coppie in quadratura.

Se analizziamo singolarmente la coppia Lei Leone-Lui Scorpione, riscontriamo una deviazione del -0,47% ma non sappiamo se questo dipende da un caso, se invece la analizziamo alla luce dei risultati degli altri 23 tipi di coppie dello stesso tipo, capiamo che quell'esiguo -0,47% non era il risultato di un caso, ma che indica una reale tendenza ad evitarsi delle coppie di questo tipo.

Le deviazioni riscontrate sulle 144 coppie sono tutte molto piccole. Il valore più alto è quello delle coppie Capricorno-Capricorno che è del 2,6%. Ma si tratta comunque di deviazioni molto più alte di quelle che si possono verificare per caso. Ad esempio, non c'è alcun dubbio che l'eccesso riscontrato sulle coppie dello stesso segno, non sia dovuto ad un caso. Le deviazioni per le coppie Ariete-Ariete, Toro-Toro, Gemelli-Gemelli ecc. sicuramente non sono l'effetto di un caso, e nemmeno sono il risultato di un errore di risposta sistematico che era stato ipotizzato da Voas ma che è smentito dal suo crucial test. Dopo che questo è stato effettivamente eseguito.

Poi ci sono altre 15 coppie che mostrano delle deviazioni significative anche se prese singolarmente.

Però come dice Voas, non possiamo prendere queste deviazioni troppo sul serio, perché sono molto piccole, e sono basate su dei dati che non sempre sono accurati, e che presentano delle vistose anomalie, come quella del surplus delle persone nate il 1 gennaio.

Di questo surplus sia Voas che io ne abbiamo tenuto conto, ma ci potrebbero essere anche degli altri errori nei dati non ancora evidenziati, che potrebbero portare a delle deviazioni, specialmente se, come nel nostro caso, queste deviazioni sono piuttosto piccole in termini percentuali.

Però lo scenario muta completamente se analizziamo le coppie in funzione degli aspetti formati dai segni di nascita dei coniugi.

Tra tutti gli aspetti possibili ce ne sono alcuni che si discostano in modo estremamente significativo da quelli che sarebbero i valori previsti.

Questi aspetti sono la congiunzione che è molto positiva, e il quinconce, la quadratura e l'opposizione che sono al contrario negativi.

Ma se parliamo di congiunzioni, quinconce, quadrature, e opposizioni stiamo parlando di astrologia.

Questo test basato su 20 milioni di soggetti, l'intera popolazione sposata in Galles e in Inghilterra, dimostra che esiste una correlazione tra il matrimonio e i segni zodiacali, e che le deviazioni trovate dipendono dalla distanza angolare tra i segni, che noi astrologi chiamiamo aspetti, e che sono uno dei fondamenti dell'astrologia.

Per cui questo è il primo test al mondo che dimostra in modo inequivocabile che l'astrologia non è una fantasia, ma una realtà dimostrata scientificamente, perché il segno zodiacale di nascita influisce sul comportamento umano, e in particolare nelle scelte sentimentali.

Se i nativi dell'Ariete tendono a sposarsi con quelli del Leone ed ad evitare di sposarsi con quelli del Cancro, questo fatto implica che i nativi dell'Ariete hanno delle caratteristiche peculiari che li distinguono dai nativi degli altri segni. Se è valida la sinastria, deve essere necessariamente valido il concetto che i nativi dei vari segni zodiacali hanno delle caratteristiche diverse, e che essere del Leone non è come essere dei Pesci.

In altre parole il segno zodiacale conta, non è una classificazione priva di significato, così come credono i detrattori dell'astrologia.

Certo, alla luce di questi risultati non si può dire che i segni zodiacali contino molto.

Se prendiamo i dati delle coppie in quadratura, queste sono solo lo 0,5% in meno di quello che dovrebbero essere, e questo significa che ogni volta che ci aspetteremmo di trovare 200 coppie di questo tipo, ne troviamo soltanto 199. Per cui l'influsso astrologico riguarderebbe soltanto questa coppia che non si è sposata, ma non si manifesta sulle restanti 199 coppie che si sono regolarmente sposate.

Sulla base di questi risultati, se mi si presentasse una coppia di fidanzati in cui segni sono in quadratura, io non potrei consigliargli di non sposarsi perché la quadratura porta iella.

Ho intitolato i post precedenti: la quadratura porta iella, il quinconce e l'opposizione portano iella.

L'ho fatto perché volevo evidenziare i risultati della statistica. Perché in effetti è così, quinconce, quadratura e opposizione tra i segni di nascita di due persone, inclinano queste persone a sposarsi meno frequentemente tra di loro.

Però è anche vero che si tratta di influssi molto leggeri, e che non hanno un peso determinante nel destino delle persone.

Una delle conclusioni che si possono trarre da questa statistica, è che il segno zodiacale non è un fattore determinante per le scelte matrimoniali. Per cui quando a noi astrologi ci rivolgono la classica domanda: Come va l'Ariete con i Gemelli?
La nostra risposta dovrebbe essere: Non si può dire nulla sulla base del segno zodiacale, per dire qualcosa sulla compatibilità tra te e il tuo ragazzo, avrei bisogno di studiare i vostri temi di nascita completi.

Il segno di nascita preso isolatamente ha uno scarso valore predittivo.

Però questa statistica dimostra che sebbene questo influsso o correlazione sia piccola, questo influsso esiste, e questo non è ciò che affermano gli scettici come quelli del CICAP, perché loro dicono che non esiste alcun effetto astrologico, ma questa statistica li smentisce.

Dati Voas - Tavola n.7

Le Coppie Previste

Segni Voas

Gli Aspetti Voas

Le conclusioni di Voas

This research shows that astrological sign has no impact on the probability of marrying – and staying married to – someone of any other sign. For decades, popular astrologers have promoted the idea of ‘love signs’: compatibility between partners with certain combinations of birthdays. If the more than twenty million married people in England and Wales offer any indication, however, lonely hearts who worry about the zodiac are wasting their time.

This analysis of the birthdays of all the husbands and wives in England and Wales is the largest-scale test of astrology ever undertaken. If there is even the smallest tendency for Virgos to fancy Capricorns, or for Libras to like Leos, then we should see it in the statistics. Even if only one pair in a thousand is influenced by the stars, then with a population of ten million couples, favoured combinations of signs would in total appear an extra ten thousand times. No such evidence can be found, though. After making allowances for response error and imputation, the distribution of spousal birthdays is what one would expect from a random distribution.

Astrologers are likely to complain that full birth charts are needed to predict personality accurately. There are two responses. First, to the extent that astrology has influenced everyday belief, it is almost entirely through the use of sun signs; if those were seen as useless when it comes to assessing personality and romantic compatibility, then astrology would lose its hold on the public imagination. Secondly, the basic signs are important even in professional charts. If they had any direct influence, however small, the giant magnifying glass of this huge sample would reveal it. No effects can be detected. 

L'analisi della Tavola n.7

The distribution in Table 7 is as close to random as one is likely to find in a real-world situation. Despite the prevalence of systematic response error and the very approximate nature of the correction method, the discrepancies revealed in Table 8 are only slightly larger than would be generated by a wholly random process. With a total of 9,500,000 distributed across a 12x12 table, cell values can vary by up to 450 above or below expectation without causing the hypothesis that the row and column variables are independent to be rejected at the 0.05 level. Most of the values in Table 8 are within that range, but a scattering of exceptions (from a minimum of -680 to a maximum of 631) leads to a chi-square test result that is significant at the 0.01 level.

In view of the enormous sample size and the imperfections in the data, this statistical outcome has no substantive significance. The difficulty with small samples is that nothing is statistically significant, even when genuine effects are at work; the problem with very large samples is that everything is statistically significant, even when the background is merely noise. The deviations are tiny relative to the number of couples with each combination of signs; from the 144 pairs, the largest gap between the actual count and what one would expect is barely 1%.

L'analisi della tavola n.7 è errata e di conseguenza sono errate le conclusioni di Voas. Lui nota che tra le 144 combinazioni dei segni, ce ne sono alcune statisticamente significative, ma non gli da molta importanza, perché su una statistica su larga scala, e basata su dei dati non molto affidabili, è facile trovare dei falsi positivi. E su questo potrebbe avere ragione. 

Però a lui non viene in mente di raggruppare le 144 coppie in base all'aspetto.

L'ultima delle Tavole presente su questa pagina, è stata fatta con i dati Voas, ma sono stata io a farla e non Voas.

Questa ultima tavola mostra in modo evidentissimo che le coppie analizzate in base all'aspetto formato tra i segni dei coniugi hanno un andamento simile.

Nonostante la sua "correzione" le coppie degli aspetti 3, 5, e 6 sono meno del previsto, e le coppie degli aspetti 0, 1, e 4 sono più del previsto.

Una distribuzione del genere è con tutta evidenza una distribuzione non casuale.

Se si prende una singola coppia, come ad esempio la coppia lei Cancro - lui Sagittario, la deviazione tra il numero previsto e quello trovato, anche nel caso che sia statisticamente significativa non può essere presa troppo sul serio. Ma le cose cambiano se si analizzano nel loro insieme tutte le coppie dello stesso tipo, ossia tutte le coppie che come quella del Cancro e Sagittario condividono lo stesso aspetto.

Le coppie in quinconce sono 24, e se sommiamo i valori trovati e i valori previsti di queste 24 coppie, otteniamo che il totale previsto per le coppie in quinconce era di 1580514 e che il totale osservato è stato invece di 1574720.

La deviazione trovata è altamente significativa, sebbene sia percentualmente piuttosto piccola.

Questo 0,37% in meno delle coppie in quinconce, non ci dovrebbe essere se i segni zodiacali non c'entrassero nulla con le scelte matrimoniali.

Ci sono solo 4 probabilità su 10 milioni che una simile deviazione si verifichi per puro caso.

Lo stesso Voas riconoscerebbe che non si tratta di una deviazione casuale, il problema è che lui non ha provato a raggruppare le 144 coppie in base agli aspetti formati tra i segni dei coniugi.

Ed è per questo che la sua tavola n.7 gli appare nel complesso scarsamente significativa, mentre è in realtà estremamente significativa.